Zadanie
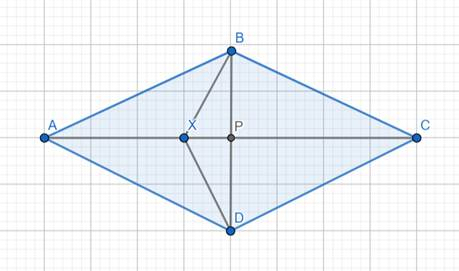
Narysowano romb ABCD oraz jego przekątne przecinające się w punkcie P. Umieszczono punkt X w dowolnym miejscu odcinka AP. Udowodnij, że trójkąty ABX i ADX są przystające.
Rozwiązanie
|AB|=|AD|
Trójkąty mają wspólny bok AX
Trójkąty przystające z cechy bok-kąt-bok
Wyjaśnienie
Zauważ, że romb ma wszystkie boki równej długości, więc długości odcinków AB i AD są sobie równe. Dodatkowo kąty między przekątną a bokiem również są równe z własności rombu. Wystarczy zauważyć, że trójkąty te mają wspólny bok AX, czyli są przystające z cechy bok-kąt-bok.
Matematyka - wybrane pytania
REKLAMA
Zadania z tego działu
IV. Wielokąty
69
1. Figury przystające
69
Zadanie 5.
69Zadanie 7.
69Zadanie 9.
70Zadanie 15.
70Zadanie 21.
71Zadanie 23.
71
2. Cechy przystawania trójkątów
72
Zadanie 1.
72Zadanie 8.
73Zadanie 9.
73Zadanie 10.
73Zadanie 11.
73
3. Przystawanie trójkątów w dowodach twierdzeń
75
Zadanie 3.
75Zadanie 7.
75Zadanie 13.
76
4. Wielokąty foremne
78
Zadanie 3.
78Zadanie 7.
78Zadanie 16.
79Zadanie 22.
80
Powtórzenie IV
81
Zadanie 5.
81Zadanie 6.
81Zadanie 15.
83Zadanie 17.
83
Jak na egzaminie
84