W zadaniu musisz określić wartości rzeczywiste parametru m, dla których przedstawione równanie ma jedno rozwiązanie.
![]()
Wprowadź zmienną pomocniczą:
![]()
![]()
![]() – warunki
– warunki
Warunek I
![]()
![]()
![]()
![]()
![]()
![]()
Czyli dla
![]() równanie kwadratowe
równanie kwadratowe
![]() ma jedno rozwiązanie równe:
ma jedno rozwiązanie równe:
![]()
Rozwiązanie to będzie dodatnie dla:
![]()
![]()
Czyli dla
![]() rozwiązanie równania jest dodatnie. Ostatecznie:
rozwiązanie równania jest dodatnie. Ostatecznie:
![]()
Czyli dla
![]() równanie ma jedno rozwiązanie.
równanie ma jedno rozwiązanie.
Warunek II
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Czyli dla
![]() iloczyn
iloczyn
![]() . Ostatecznie:
. Ostatecznie:
![]()
Czyli dla
![]() równanie ma dwa rozwiązania, z których jedno jest ujemne – czyli po uwzględnieniu dziedziny, równanie ma tylko jedno rozwiązanie.
równanie ma dwa rozwiązania, z których jedno jest ujemne – czyli po uwzględnieniu dziedziny, równanie ma tylko jedno rozwiązanie.
III warunek
![]() dla
dla
![]() .
.
![]()
![]()
![]()
Czyli dla
![]() suma
suma
![]() .
.
![]()
![]()
![]()
![]()
![]()
Czyli dla
![]() iloczyn
iloczyn
![]() .
.
Ostatecznie:
![]()
Nie istnieje m, dla którego równanie ma dwa rozwiązania, z których jedno wynosi 0.
Ostateczna odpowiedź:
![]()

Na początku zauważ, że:
![]()
Wprowadź zmienną pomocniczą:
![]()
Zapisz równanie ze zmienną pomocniczą:
![]()
Aby równanie kwadratowe miało jedno rozwiązanie, muszą być spełnione następujące warunki:
![]()
Założenie
![]() warunkuje, że jedno z dwóch rozwiązań będzie ujemne, czyli nie będzie należało do dziedziny równania. Założenia
warunkuje, że jedno z dwóch rozwiązań będzie ujemne, czyli nie będzie należało do dziedziny równania. Założenia
![]() gwarantują, że jedno z rozwiązań będzie równe 0, czyli nie będzie należeć do dziedziny równania.
gwarantują, że jedno z rozwiązań będzie równe 0, czyli nie będzie należeć do dziedziny równania.
Zacznij od wyznaczenia
![]() :
:
![]()
Sprawdź, dla jakich wartości parametru m
![]() :
:
![]()
![]()
![]()
![]()
![]()
Czyli dla
![]() równanie kwadratowe
równanie kwadratowe
![]() ma jedno rozwiązanie równe:
ma jedno rozwiązanie równe:
![]()
Znajdź wartości parametru m, dla których rozwiązanie to będzie dodatnie:
![]()
![]()
Czyli dla
![]() rozwiązanie równania jest dodatnie. Znajdź część wspólną obu przedziałów:
rozwiązanie równania jest dodatnie. Znajdź część wspólną obu przedziałów:
![]()
Czyli dla
![]() równanie ma jedno rozwiązanie.
równanie ma jedno rozwiązanie.
Rozważ kolejny przypadek, czyli przypadek, w którym
![]() oraz
oraz
![]() . Najpierw sprawdź, dla jakich wartości parametru m
. Najpierw sprawdź, dla jakich wartości parametru m
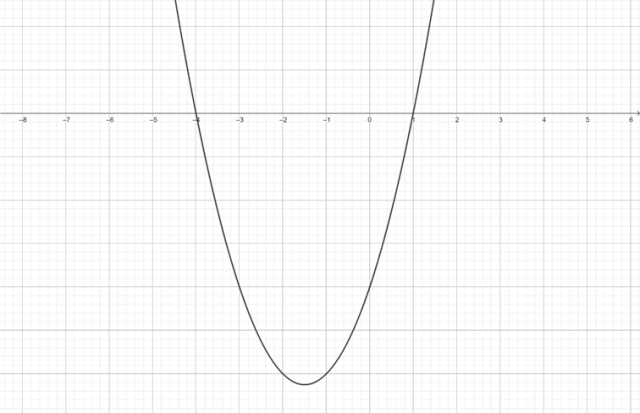
![]() . W tym celu narysuj wykres funkcji,
. W tym celu narysuj wykres funkcji,
![]() korzystając z poprzednich obliczeń miejsc zerowych:
korzystając z poprzednich obliczeń miejsc zerowych:
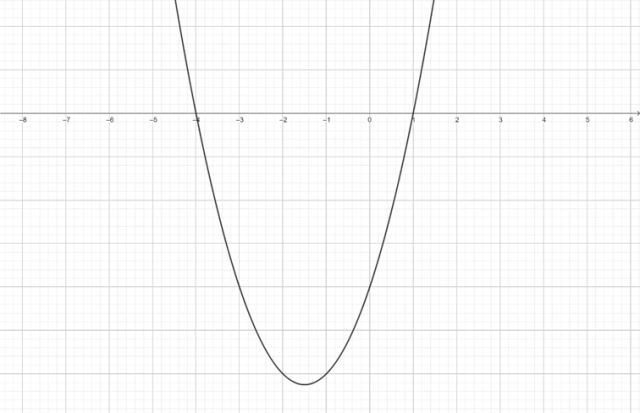
Z wykresu odczytaj, dla jakich argumentów funkcja przyjmuje wartości dodatnie:
![]()
Następnie sprawdź, dla jakich wartości
![]() . W tym celu skorzystaj ze wzorów Viete’a:
. W tym celu skorzystaj ze wzorów Viete’a:
![]()
![]()
![]()
![]()
![]()
Czyli dla
![]() iloczyn
iloczyn
![]() . Znajdź część wspólną obu znalezionych przedziałów:
. Znajdź część wspólną obu znalezionych przedziałów:
![]()
Czyli dla
![]() równanie ma dwa rozwiązania, z których jedno jest ujemne – czyli po uwzględnieniu dziedziny, równanie ma tylko jedno rozwiązanie.
równanie ma dwa rozwiązania, z których jedno jest ujemne – czyli po uwzględnieniu dziedziny, równanie ma tylko jedno rozwiązanie.
Rozważ ostatni przypadek, w którym muszą być spełnione warunki:
![]()
![]() dla
dla
![]() .
.
Sprawdź, dla jakich wartości
![]() . W tym celu skorzystaj ze wzorów Viete’a:
. W tym celu skorzystaj ze wzorów Viete’a:
![]()
![]()
![]()
Czyli dla
![]() suma
suma
![]() .
.
Sprawdź, dla jakich wartości
![]() :
:
![]()
![]()
![]()
![]()
Czyli dla
![]() iloczyn
iloczyn
![]() .
.
Znajdź część wspólną przedziałów znalezionych podczas rozpatrywania ostatniego przypadku:
![]()
Czyli nie istnieje m, dla którego równanie ma dwa rozwiązania, z których jedno wynosi 0.
Aby sformułować ostateczną odpowiedź, znajdź sumę wszystkich znalezionych w rozpatrywanych przypadkach przedziałów:
![]()

Ćwiczenie 2.
7Ćwiczenie 3.
8Ćwiczenie 4.
8Ćwiczenie 8.
11Zadanie 1.
13Zadanie 2.
13Zadanie 3.
14Zadanie 4.
14Zadanie 6.
14Zadanie 7.
14Zadanie 8.
14Zadanie 9.
15Zadanie 10.
15Zadanie 14.
15Zadanie 15.
15Ćwiczenie 2.
19Zadanie 1.
23Zadanie 2.
23Zadanie 3.
24Zadanie 4.
24Zadanie 5.
24Zadanie 6.
24Zadanie 7.
24Zadanie 8.
24Zadanie 9.
24Ćwiczenie 1.
26Ćwiczenie 2.
27Ćwiczenie 3.
28Ćwiczenie 4.
28Zadanie 1.
31Zadanie 2.
31Zadanie 3.
31Zadanie 4.
32Zadanie 5.
32Zadanie 6.
32Zadanie 7.
32Zadanie 8.
32Zadanie 10.
32Zadanie 11.
32Ćwiczenie 1.
34Ćwiczenie 2.
35Zadanie 1.
39Zadanie 2.
39Zadanie 3.
39Zadanie 4.
39Zadanie 5.
40Zadanie 6.
40Zadanie 7.
40Zadanie 8.
40Zadanie 9.
40Zadanie 10.
40Ćwiczenie 1.
43Ćwiczenie 3.
44Zadanie 1.
47Zadanie 2.
47Zadanie 3.
47Zadanie 4.
47Zadanie 5.
48Zadanie 6.
48Zadanie 7.
48Zadanie 8.
48Zadanie 9.
48Zadanie 10.
48Zadanie 11.
48Zadanie 2.
53Zadanie 9.
55Zadanie 10.
55Zadanie 11.
55Zadanie 12.
55Zadanie 13.
55Zadanie 14.
55Zadanie 15.
55Zadanie 18.
56Zadanie 19.
56Zadanie 21.
56Zadanie 22.
56
