W zadaniu musisz rozwiązać nierówność
![]() .
.
Dziedzina:
![]()
![]()
![]()
![]()
![]()
Zatem
![]() jest dziedziną nierówności.
jest dziedziną nierówności.
![]() - suma szeregu geometrycznego zbieżnego gdzie
- suma szeregu geometrycznego zbieżnego gdzie
![]() ,
,
![]() .
.
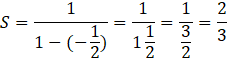
Nierówność przyjmuje więc postać:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Uwzględnij dziedzinę:
![]()
Zatem
![]() .
.

Na początku wyznacz dziedzinę nierówności:
![]()
![]()
Liczba
![]() jest liczbą większą od 1, a więc porównaj wykładniki, pozostawiając znak nierówności bez zmian:
jest liczbą większą od 1, a więc porównaj wykładniki, pozostawiając znak nierówności bez zmian:
![]()
![]()
![]()
Zatem
![]() jest dziedziną nierówności.
jest dziedziną nierówności.
Zauważ, że po prawej stronie nierówności w wykładniku potęgi możesz skorzystać ze wzoru na sumę szeregu geometrycznego zbieżnego:
![]()
gdzie pierwszy wyraz szeregu
![]() , natomiast iloraz
, natomiast iloraz
![]() .
.
Otrzymujesz zatem:
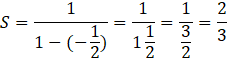
Nierówność możesz zapisać więc następująco:
![]()
Obie strony nierówności są większe bądź równe 0, a więc możesz podnieść je do kwadratu:
![]()
Sprowadź nierówność do jak najprostszej postaci:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Nierówność jest spełniona dla każdej liczby rzeczywistej x, ponieważ
![]() , zatem:
, zatem:
![]()
Uwzględnij dziedzinę:
![]()

Ćwiczenie 2.
7Ćwiczenie 3.
8Ćwiczenie 4.
8Ćwiczenie 8.
11Zadanie 1.
13Zadanie 2.
13Zadanie 3.
14Zadanie 4.
14Zadanie 6.
14Zadanie 7.
14Zadanie 8.
14Zadanie 9.
15Zadanie 10.
15Zadanie 14.
15Zadanie 15.
15Ćwiczenie 2.
19Zadanie 1.
23Zadanie 2.
23Zadanie 3.
24Zadanie 4.
24Zadanie 5.
24Zadanie 6.
24Zadanie 7.
24Zadanie 8.
24Zadanie 9.
24Ćwiczenie 1.
26Ćwiczenie 2.
27Ćwiczenie 3.
28Ćwiczenie 4.
28Zadanie 1.
31Zadanie 2.
31Zadanie 3.
31Zadanie 4.
32Zadanie 5.
32Zadanie 6.
32Zadanie 7.
32Zadanie 8.
32Zadanie 10.
32Zadanie 11.
32Ćwiczenie 1.
34Ćwiczenie 2.
35Zadanie 1.
39Zadanie 2.
39Zadanie 3.
39Zadanie 4.
39Zadanie 5.
40Zadanie 6.
40Zadanie 7.
40Zadanie 8.
40Zadanie 9.
40Zadanie 10.
40Ćwiczenie 1.
43Ćwiczenie 3.
44Zadanie 1.
47Zadanie 2.
47Zadanie 3.
47Zadanie 4.
47Zadanie 5.
48Zadanie 6.
48Zadanie 7.
48Zadanie 8.
48Zadanie 9.
48Zadanie 10.
48Zadanie 11.
48Zadanie 2.
53Zadanie 9.
55Zadanie 10.
55Zadanie 11.
55Zadanie 12.
55Zadanie 13.
55Zadanie 14.
55Zadanie 15.
55Zadanie 18.
56Zadanie 19.
56Zadanie 21.
56Zadanie 22.
56
