W zadaniu musisz rozwiązać graficznie nierówność.
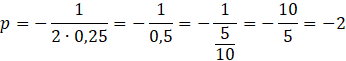
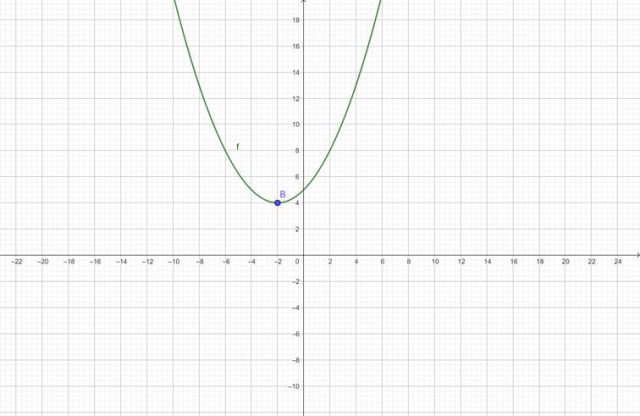
Zatem wykres funkcji
wygląda następująco:
Następnie narysuj wykres funkcji
:
| x | -1 | 0 | 2 |
| y | 2 | 1 |
|
Zatem:
Aby rozwiązać tę nierówność, musisz znaleźć argumenty, dla których funkcja kwadratowa
jest większa bądź równa funkcji wykładniczej
.
Zacznij od narysowania wykresu funkcji kwadratowej. W tym celu oblicz najpierw współrzędne wierzchołka:
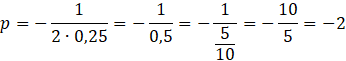
Współczynnik stojący przy
jest liczbą dodatnią, zatem parabola ma ramiona skierowane w górę. Możesz narysować jej wykres:
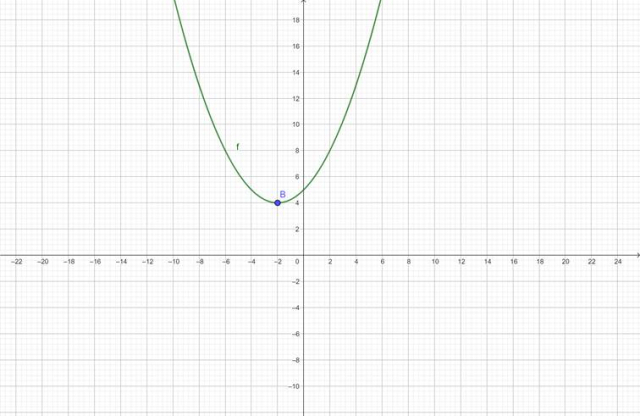
Teraz w tym samym układzie współrzędnych narysuj wykres funkcji wykładniczej
. W łatwy sposób zrobisz to, znajdując 3 punkty, należące do wykresu tej funkcji:
| x | -1 | 0 | 2 |
| y | 2 | 1 |
|
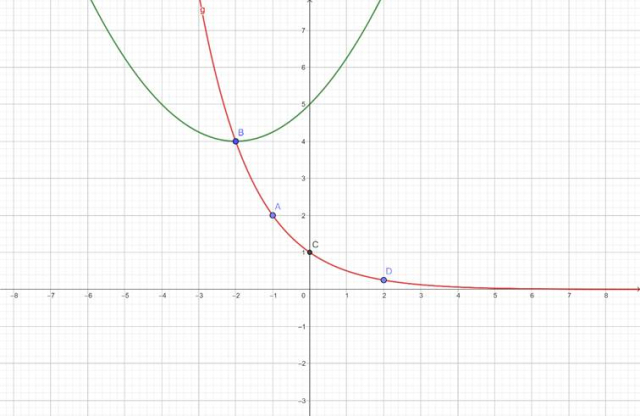
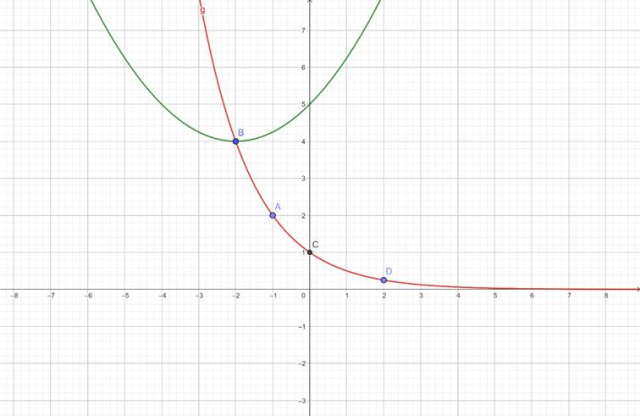
Z wykresu odczytaj, dla jakich argumentów narysowana funkcja kwadratowa jest większa bądź równa wykładniczej:
Ćwiczenie 2.
7Ćwiczenie 3.
8Ćwiczenie 4.
8Ćwiczenie 8.
11Zadanie 1.
13Zadanie 2.
13Zadanie 3.
14Zadanie 4.
14Zadanie 6.
14Zadanie 7.
14Zadanie 8.
14Zadanie 9.
15Zadanie 10.
15Zadanie 14.
15Zadanie 15.
15Ćwiczenie 2.
19Zadanie 1.
23Zadanie 2.
23Zadanie 3.
24Zadanie 4.
24Zadanie 5.
24Zadanie 6.
24Zadanie 7.
24Zadanie 8.
24Zadanie 9.
24Ćwiczenie 1.
26Ćwiczenie 2.
27Ćwiczenie 3.
28Ćwiczenie 4.
28Zadanie 1.
31Zadanie 2.
31Zadanie 3.
31Zadanie 4.
32Zadanie 5.
32Zadanie 6.
32Zadanie 7.
32Zadanie 8.
32Zadanie 10.
32Zadanie 11.
32Ćwiczenie 1.
34Ćwiczenie 2.
35Zadanie 1.
39Zadanie 2.
39Zadanie 3.
39Zadanie 4.
39Zadanie 5.
40Zadanie 6.
40Zadanie 7.
40Zadanie 8.
40Zadanie 9.
40Zadanie 10.
40Ćwiczenie 1.
43Ćwiczenie 3.
44Zadanie 1.
47Zadanie 2.
47Zadanie 3.
47Zadanie 4.
47Zadanie 5.
48Zadanie 6.
48Zadanie 7.
48Zadanie 8.
48Zadanie 9.
48Zadanie 10.
48Zadanie 11.
48Zadanie 2.
53Zadanie 9.
55Zadanie 10.
55Zadanie 11.
55Zadanie 12.
55Zadanie 13.
55Zadanie 14.
55Zadanie 15.
55Zadanie 18.
56Zadanie 19.
56Zadanie 21.
56Zadanie 22.
56