W zadaniu musisz narysować wykres funkcji
![]() , a następnie obliczyć współrzędne punktu wspólnego dla funkcji g oraz osi OY.
, a następnie obliczyć współrzędne punktu wspólnego dla funkcji g oraz osi OY.
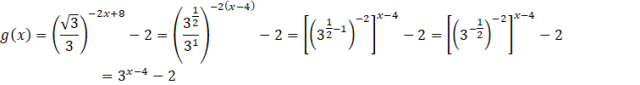
Wykres funkcji
![]() :
:
| x | -1 | 0 | 1 | 2 |
| Y |
| 1 | 3 | 9 |
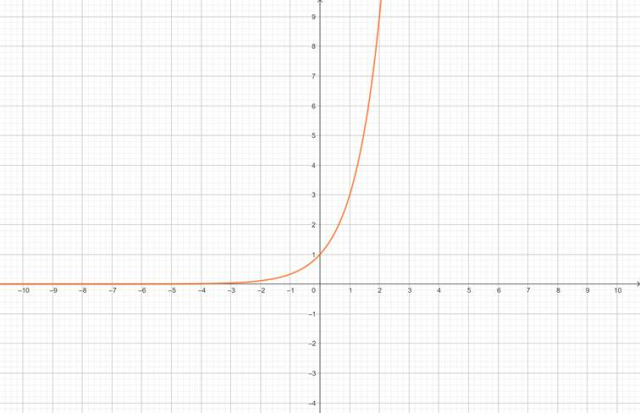
Wykres funkcji g:
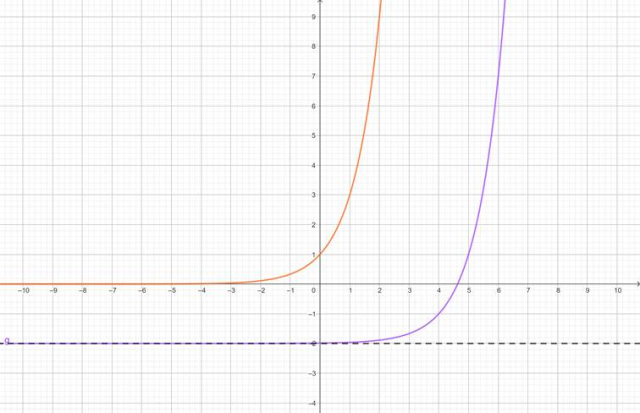
![]()
Punkt wspólny wykresu funkcji g i osi OY ma zatem współrzędne
![]() .
.

Na początku zauważ, że:
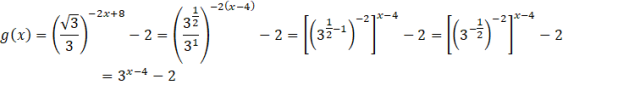
Aby zatem otrzymać wykres funkcji g, zacznij od narysowania wykresu funkcji wykładniczej
![]() . W tym celu znajdź kilka charakterystycznych punktów tej funkcji:
. W tym celu znajdź kilka charakterystycznych punktów tej funkcji:
| X | -1 | 0 | 1 | 2 |
| Y |
| 1 | 3 | 9 |
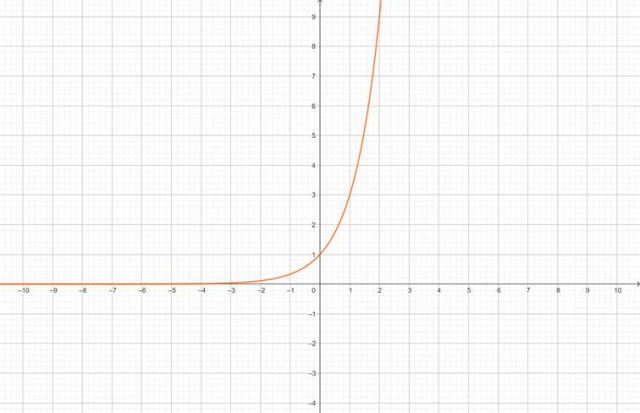
Następnie, aby otrzymać wykres funkcji g, przesuń wykres funkcji
![]() o 4 jednostki w prawo równolegle wzdłuż osi OX oraz 2 jednostki w dół równolegle wzdłuż osi OY:
o 4 jednostki w prawo równolegle wzdłuż osi OX oraz 2 jednostki w dół równolegle wzdłuż osi OY:
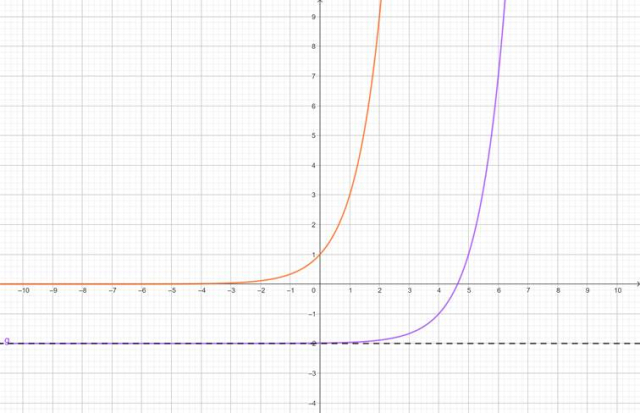
Pierwsza współrzędna punktu wspólnego wykresu funkcji g z osią OY wynosi 0. Aby znaleźć drugą współrzędną, musisz zatem obliczyć wartość funkcji dla argumentu
![]()
![]()
Punkt wspólny wykresu funkcji g i osi OY ma zatem współrzędne
![]() .
.

Ćwiczenie 2.
7Ćwiczenie 3.
8Ćwiczenie 4.
8Ćwiczenie 8.
11Zadanie 1.
13Zadanie 2.
13Zadanie 3.
14Zadanie 4.
14Zadanie 6.
14Zadanie 7.
14Zadanie 8.
14Zadanie 9.
15Zadanie 10.
15Zadanie 14.
15Zadanie 15.
15Ćwiczenie 2.
19Zadanie 1.
23Zadanie 2.
23Zadanie 3.
24Zadanie 4.
24Zadanie 5.
24Zadanie 6.
24Zadanie 7.
24Zadanie 8.
24Zadanie 9.
24Ćwiczenie 1.
26Ćwiczenie 2.
27Ćwiczenie 3.
28Ćwiczenie 4.
28Zadanie 1.
31Zadanie 2.
31Zadanie 3.
31Zadanie 4.
32Zadanie 5.
32Zadanie 6.
32Zadanie 7.
32Zadanie 8.
32Zadanie 10.
32Zadanie 11.
32Ćwiczenie 1.
34Ćwiczenie 2.
35Zadanie 1.
39Zadanie 2.
39Zadanie 3.
39Zadanie 4.
39Zadanie 5.
40Zadanie 6.
40Zadanie 7.
40Zadanie 8.
40Zadanie 9.
40Zadanie 10.
40Ćwiczenie 1.
43Ćwiczenie 3.
44Zadanie 1.
47Zadanie 2.
47Zadanie 3.
47Zadanie 4.
47Zadanie 5.
48Zadanie 6.
48Zadanie 7.
48Zadanie 8.
48Zadanie 9.
48Zadanie 10.
48Zadanie 11.
48Zadanie 2.
53Zadanie 9.
55Zadanie 10.
55Zadanie 11.
55Zadanie 12.
55Zadanie 13.
55Zadanie 14.
55Zadanie 15.
55Zadanie 18.
56Zadanie 19.
56Zadanie 21.
56Zadanie 22.
56
