W zadaniu musisz rozwiązać nierówność
![]() .
.
Dziedzina:
![]()
![]()
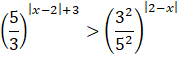
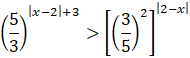
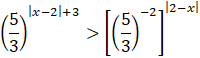
![]()
![]()
![]()
![]()
![]() , zatem:
, zatem:
![]()
![]()
![]()
![]()
Wartość bezwzględna jakiejkolwiek liczby rzeczywistej jest zawsze liczbą nieujemną, zatem
![]() .
.

Na początku wyznacz dziedzinę nierówności:
![]()
Zapisz obie strony nierówności w postaci potęg o tej samej podstawie. W tym celu skorzystaj z własności potęg o wykładnikach rzeczywistych.
![]()
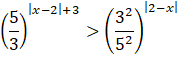
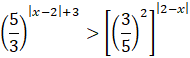
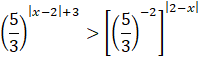
![]()
Liczba
![]() jest liczbą większą od 1, a więc porównaj wykładniki, pozostawiając znak nierówności bez zmian:
jest liczbą większą od 1, a więc porównaj wykładniki, pozostawiając znak nierówności bez zmian:
![]()
![]()
![]()
![]() , zatem otrzymujesz:
, zatem otrzymujesz:
![]()
![]()
![]()
![]()
Wartość bezwzględna jakiejkolwiek liczby rzeczywistej jest zawsze liczbą nieujemną, zatem nierówność ta jest spełniona dla
![]() .
.

Ćwiczenie 2.
7Ćwiczenie 3.
8Ćwiczenie 4.
8Ćwiczenie 8.
11Zadanie 1.
13Zadanie 2.
13Zadanie 3.
14Zadanie 4.
14Zadanie 6.
14Zadanie 7.
14Zadanie 8.
14Zadanie 9.
15Zadanie 10.
15Zadanie 14.
15Zadanie 15.
15Ćwiczenie 2.
19Zadanie 1.
23Zadanie 2.
23Zadanie 3.
24Zadanie 4.
24Zadanie 5.
24Zadanie 6.
24Zadanie 7.
24Zadanie 8.
24Zadanie 9.
24Ćwiczenie 1.
26Ćwiczenie 2.
27Ćwiczenie 3.
28Ćwiczenie 4.
28Zadanie 1.
31Zadanie 2.
31Zadanie 3.
31Zadanie 4.
32Zadanie 5.
32Zadanie 6.
32Zadanie 7.
32Zadanie 8.
32Zadanie 10.
32Zadanie 11.
32Ćwiczenie 1.
34Ćwiczenie 2.
35Zadanie 1.
39Zadanie 2.
39Zadanie 3.
39Zadanie 4.
39Zadanie 5.
40Zadanie 6.
40Zadanie 7.
40Zadanie 8.
40Zadanie 9.
40Zadanie 10.
40Ćwiczenie 1.
43Ćwiczenie 3.
44Zadanie 1.
47Zadanie 2.
47Zadanie 3.
47Zadanie 4.
47Zadanie 5.
48Zadanie 6.
48Zadanie 7.
48Zadanie 8.
48Zadanie 9.
48Zadanie 10.
48Zadanie 11.
48Zadanie 2.
53Zadanie 9.
55Zadanie 10.
55Zadanie 11.
55Zadanie 12.
55Zadanie 13.
55Zadanie 14.
55Zadanie 15.
55Zadanie 18.
56Zadanie 19.
56Zadanie 21.
56Zadanie 22.
56
