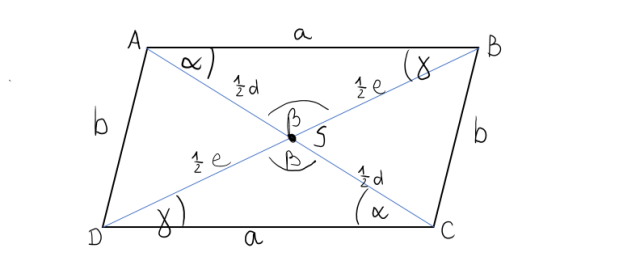
Wynika z rysunku, że trójkąty ABS i DCS są przystające.
Zatem długości boków AB i CD są sobie równe oraz długości boków AC i BC są również sobie równe, co należało dowieść.

Narysuj dany równoległobok, zaznacz równe odcinki, które powstały poprzez przecięcie się przekątnych. Zauważ, że trójkąty ABS i CDS są przystające, zatem długości boków AB i CD oraz AD i BC są sobie równe. Co oznacza, że czworokąt jest równoległobokiem.