W tym zadaniu oblicz pole poprzecznego dębowej belki o masie m = 368 kg i długości l = 8 m, jeśli po zanurzeniu w wodzie jej ciężar pozornie zmniejsza się o 86%. Przyjmij gęstość wody ![]()
Siła wyporu jest różnicą ciężaru belki przed i po zanurzeniu:
![]()
I z definicji:
![]()
Więc:
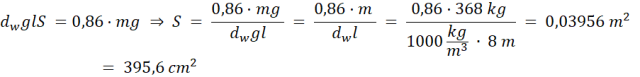
Odpowiedź: Belka ma pole powierzchni równe ![]()

Korzystamy ze wzoru na siłę wyporu i faktu, że utracony przez zanurzenie ciężar jest równy sile wyporu wody. Przyrównujemy do siebie wzory i wyznaczamy pole powierzchni.

Przykład Przykład 1.
11Przykład Przykład 2.
12Przykład Przykład 3.
13Zadanie 7.1.2
14Zadanie 7.1.3
14Zadanie 7.1.5
15Zadanie 7.1.8
15Zadanie 7.1.9
15Przykład Przykład 1.
16Zadanie 7.2.1.
18Zadanie 7.2.3.
19Zadanie 7.2.12.
21Zadanie 7.2.13.
21Zadanie 7.3.2.
26Zadanie 7.4.1.
30Zadanie 7.4.11.
31Przykład Przykład 1.
32Przykład Przykład 3.
34Przykład Przykład 5.
37Zadanie 7.5.4.
38Zadanie 7.5.10.
39Zadanie 7.5.14.
40Zadanie 7.5.16.
40Zadanie 7.5.20.
41Zadanie 7.5.26.
42Przykład Przykład 1.
43Zadanie 7.6.2.
46Zadanie 7.6.6.
47Przykład Przykład 2.
49Zadanie 7.7.2.
52Zadanie 7.7.3.
52Zadanie 7.7.4.
53Zadanie 7.7.6.
53Przykład Przykład 1.
55Zadanie 7.8.7.
58Przykład Przykład. Gejzer
64Zadanie Zadanie 1. Śluza
66Zadanie Zadanie 2. Balon
67Zadanie Zadanie 3. Butla z gazem
67Zadanie Zadanie 4. Wartość energetyczna pożywienia
68
