W tym zadaniu musisz określić minimalny i maksymalny współczynnik kierunkowy, wiedząc, iż prosta będąca wykresem funkcji ![]()
![]()
![]()
![]()
Czyli:
![]()
Następnie:
![]()
![]()
![]()
Ostatecznie, funkcja ma przynajmniej jeden punkt wspólny z prostokątem ABCD wtedy, gdy jej współczynnik kierunkowy zawiera się w przedziale ![]()

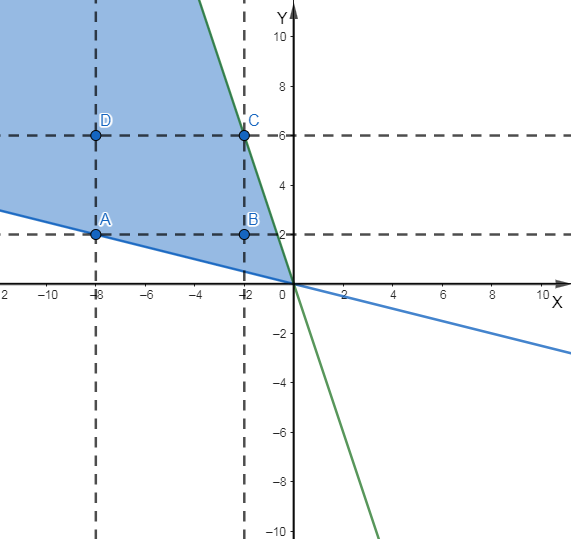
Wyraz wolny wynosi 0. Z rysunku zauważ, iż funkcja ma przynajmniej jeden punkt wspólny, gdy wartość jej współczynnika kierunkowego zawiera się między wartościami współczynników kierunkowych funkcji, w których skład wchodzą punkty A lub C:
![]()
Stąd współczynnik kierunkowy pierwszej funkcji. Otrzymujesz tym samym pierwszą z funkcji ograniczających:
![]()
Druga funkcja ograniczająca analogicznie:
![]()
Czyli ![]()

Ćwiczenie 8.
263Zadanie 1.
265Zadanie 2.
265Zadanie 3.
265Zadanie 4.
265Zadanie 5.
265Zadanie 11.
266Zadanie 12.
266Zadanie 14.
266Zadanie 15.
266Zadanie 1.
277Zadanie 2.
277Zadanie 3.
278Zadanie 4.
278Zadanie 5.
278Zadanie 6.
278Zadanie 7.
278Zadanie 6.
284Zadanie 8.
284Zadanie 1.
291Zadanie 2.
291Zadanie 3.
291Zadanie 1.
302Zadanie 2.
302Zadanie 6.
302Zadanie 1.
308Zadanie 2.
308
