Z dwóch przystani – K i L – na jezioro wypłynęły kajaki. Z przystani L wypłynęło ich mniej, niż dwa razy tyle, co wypłynęło z przystani K. Jednakże, gdyby z przystani K wypłynęły o dwa kajaki więcej, a z przystani L o dwa kajaki mniej, to z przystani L wypłynęłoby więcej kajaków niż z przystani K. Oblicz, jak wiele kajaków wypłynęło z każdej z przystani, wiedząc, iż łącznie wypłynęło ich mniej niż 18.
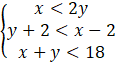
Znajdujemy następnie punkty będące rozwiązaniem każdej z par równań:
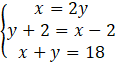
Otrzymujemy 3 układy równań:
![]()
![]()
![]()
Rozwiązaniem są 3 punkty, które tworzą trójkąt:
![]()
Rozwiązanie ogólne nierówności wyjściowej to wnętrze tego trójkąta bez brzegu. Rozwiązanie szczególne to takie, którego współrzędne będą liczbami naturalnymi (gdyż zliczamy liczbę kajaków). Jedyny punkt spełniający te warunki, to ![]()
Z przystani L wypłynęło 11 kajaków, zaś z przystani K – 6.


Oznacz przez x liczbę kajaków wypływających z przystani L. Z przystani K wypłynęło ich y i jednocześnie mniej niż ![]()


Ćwiczenie 8.
263Zadanie 1.
265Zadanie 2.
265Zadanie 3.
265Zadanie 4.
265Zadanie 5.
265Zadanie 11.
266Zadanie 12.
266Zadanie 14.
266Zadanie 15.
266Zadanie 1.
277Zadanie 2.
277Zadanie 3.
278Zadanie 4.
278Zadanie 5.
278Zadanie 6.
278Zadanie 7.
278Zadanie 6.
284Zadanie 8.
284Zadanie 1.
291Zadanie 2.
291Zadanie 3.
291Zadanie 1.
302Zadanie 2.
302Zadanie 6.
302Zadanie 1.
308Zadanie 2.
308
