Z treści zadania wiemy, że:
![]()
![]()
![]()
![]()
![]()
![]()
Szukane:
![]() ,
,
![]()
![]()
![]()
![]()
Energię kinetyczną
![]() . Można ją wyrazić jako:
. Można ją wyrazić jako:
![]() , gdzie
, gdzie
![]() - masa cząstki,
- masa cząstki,
![]() - prędkość.
- prędkość.
Pole elektryczne
![]() powoduje przyrost energii kinetycznej cząstki:
powoduje przyrost energii kinetycznej cząstki:
![]() , gdzie
, gdzie
![]() to jego napięcie.
to jego napięcie.
Zatem szybkość z jaką cząstka wpadnie w obszar pola magnetycznego :
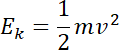
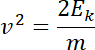
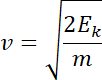
Podstawiając
![]() :
:
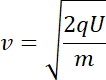
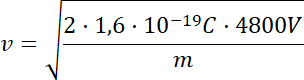
Na naładowaną cząstkę poruszającą się w obszarze pola magnetycznego działa siła magnetyczna Lorentza
![]() , gdzie
, gdzie
![]() to indukcja pola magnetycznego.
to indukcja pola magnetycznego.
Cząstka zakreśla w polu magnetycznym łuk. Siła Lorentza pełni w tym procesie rolę siły dośrodkowej, którą możemy wyrazić jako:
![]() , gdzie
, gdzie
![]() to promień okręgu.
to promień okręgu.
Stąd też możemy stwierdzić, że
![]()
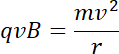
![]()
![]()
Podstawmy do wzoru
![]() ,
,
![]() z wcześniejszego obliczenia:
z wcześniejszego obliczenia:
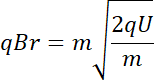
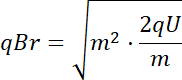
![]()
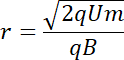
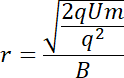
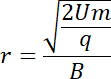
Promień toru ruchu izotopu Ne-20:
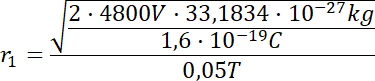


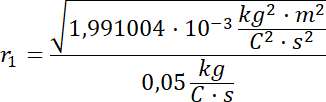
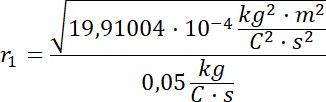
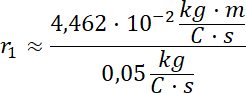
![]()
![]()
Teraz z kolei obliczamy promień toru ruchu izotopu Ne-22:
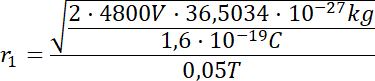


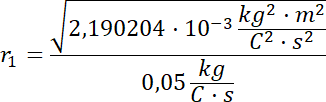
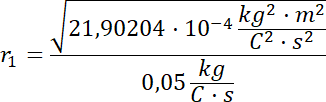
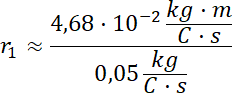
![]()
![]()

Pierwszym krokiem w rozwiązaniu tego zadania jest obliczenie mas izotopów neonu (Ne-20 i Ne-22) na podstawie dostarczonych danych o masach jednostkowych i konkretnych masach tych izotopów. Następnie, korzystając z ładunku elementarnego, obliczamy prędkości cząstek w momencie wpadania w pole magnetyczne. Wykorzystując siłę Lorentza działającą na naładowaną cząstkę, uzyskujemy zależność między promieniem toru ruchu a indukcją pola magnetycznego i napięciem pola elektrycznego. Podstawiając wartości i przeliczając jednostki, ostatecznie obliczamy promienie torów ruchu dla obu izotopów neonu.