Oblicz prędkość ostatniej kuli, wiedząc, że w jednej linii ułożone cztery identyczne bile i w skrajną kulę uderzono centralnie, wzdłuż tej prostej, kulą o prędkości v = 10 
Dane:
v = 10 
Zderzenia bil są zderzeniami sprężystymi, więc zostaje zachowana energia i pęd układu.
Zbadajmy pierwsze zderzenie – kuli poruszającej się i skrajnej, nieruchomej kuli:
niech:
v1 – prędkość uderzającej kuli po zderzeniu
v2 – prędkość nieruchomej kuli po zderzeniu
Z zasady zachowania pędu:
Z zasady zachowania energii:
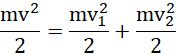
co razem daje układ równań:
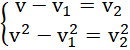
Korzystając ze wzoru skróconego mnożenia, po podzieleniu drugiego równania przez pierwsze:
ale z równania pędu:
więc:
Czyli po zderzeniu uderzająca bila przekazała całą swoją prędkość (a więc też i pęd oraz energię kinetyczną) kuli, w którą uderzyła.
Każde kolejne zderzenie przebiega identycznie – wszystkie kule mają taką samą masę i pomijamy straty prędkości wynikające z oporów ruchu.
Oznacza to, że prędkość ostatniej kuli po zderzeniu jest równa prędkości początkowej pierwszej kuli:
Odpowiedź: d) 
Zauważ, zderzenia kul bilardowych to zderzenia sprężyste – zostaje zachowany pęd i energia kinetyczna zderzających się bil. Zapisz odpowiednie równości, skróć masę (wszystkie kule mają taką samą masę m) i pomnóż drugie równanie przez 2, pozbywając się ułamka. Skorzystaj ze wzoru skróconego mnożenia a2 – b2 = (a – b)(a + b) i podziel równanie energii przez równanie pędu. Z równania pędu i otrzymanego równania liniowego stwórz układ równań. Zwróć uwagę, prędkość uderzającej kuli po zderzeniu wyniosła zero, więc cała jej prędkość została przekazana kuli uderzanej. Taki sam schemat powtórzy się jeszcze trzy razy, więc prędkość ostatniej kuli jest równa prędkości pierwszej kuli (pomijamy opory ruchu).