Oblicz masę wahadła o długości l = 1,6 m, wiedząc, że wychylono je o kąt α = 60° od położenia równowagi i puszczono je swobodnie, a w momencie, gdy wahadło ponownie znalazło się w położeniu równowagi, uderzył w niego z prędkością v = 500 
Dane:
α = 60°
l = 1,6 m
v = 500 
m = 8 g = 0,008 kg
g = 10 
Niech zwrot osi układu współrzędnych będzie zgodny z kierunkiem ruchu pocisku przed zderzeniem.
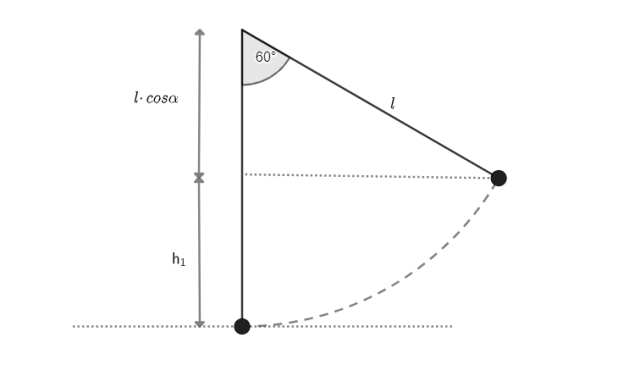
Z zasady zachowania energii dla wahadła:
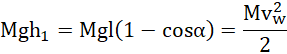
Z zasady zachowania pędu:
Zwroty wektorów prędkości nie są zgodne, więc:
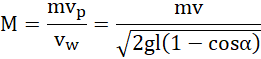
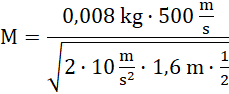
Odpowiedź: Aby wahadło zatrzymało się natychmiast po zderzeniu, jego masa musi wynosić 1 kg.
Zastosuj zasadę zachowania energii dla wahadła – w momencie wychylenia jego energia mechaniczna to energia potencjalna (iloczyn masy, przyspieszenia ziemskiego i odległości od punktu odniesienia – tutaj jest to poziom położenia równowagi), a w momencie maksymalnego powrotu do położenia równowagi jego energia mechaniczna to energia kinetyczna (iloczyn połowy masy i kwadratu prędkości). Dzięki tej równości wyznaczysz prędkość wahadła sprzed zderzenia. Następnie z zasady zachowania pędu zapisz równość pomiędzy pędem początkowym (pęd pocisku i pęd wahadła), a pędem końcowym (klocek z utkwionym pociskiem nie poruszają się, więc pęd jest zerowy). Zwróć uwagę, że wektor prędkości pocisku i wahadła są przeciwne – jeden ze składników weź ze znakiem minus. Wyznacz szukaną masę i wstaw wcześniej wyliczoną prędkość wahadła.