Oblicz prędkość trzeciej kuli po zderzeniu sprężystym, wiedząc, że trzy kule o masach kolejno: m1 = 50 g, m2 = 40 g i m3 = 60 g są zawieszone na nitkach w linii prostej, tak, by się ze sobą stykały, pierwsza z nich po odchyleniu uderzyła w drugą z prędkością v01 = 0,9 
Dane:
m1 = 50 g = 0,05 kg
m2 = 40 g = 0,04 kg
m3 = 60 g = 0,06 kg
v01 = 0,9
Niech:
v11 – prędkość kuli pierwszej po zderzeniu
v12 – prędkość kuli drugiej po uderzeniu w nią kuli pierwszej
v22 – prędkość kuli drugiej po uderzeniu w kulę trzecią
v23 – prędkość trzeciej kuli po zderzeniu z kulą drugą
Niech zwrot osi układu współrzędnych będzie zgodny z kierunkiem ruchu pierwszej kuli przed zderzeniem.
W przypadku zderzenia doskonale sprężystego po zderzeniu zostaje zachowany pęd i energia kinetyczna kul.
Etap 1. – zderzenie kuli pierwszej i drugiej:
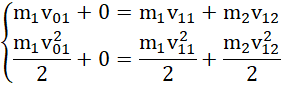
po przekształceniu:
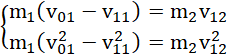
po podzieleniu równania drugiego przez pierwsze:
po wstawieniu otrzymanej równości do układu równań liniowych:
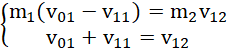
uzyskujemy:
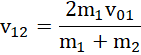
Etap 2. – zderzenie kuli drugiej i trzeciej:
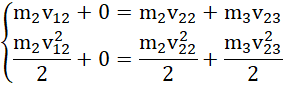
po przekształceniu:
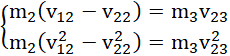
po podzieleniu równania drugiego przez pierwsze:
po wstawieniu otrzymanej równości do układu równań liniowych:
uzyskujemy:
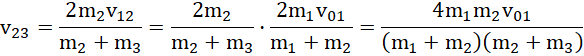
Odpowiedź: Trzecia kula po zderzeniu osiągnęła prędkość 
Pamiętaj, podczas zderzenia doskonale sprężystego zostaje zachowany pęd oraz energia kinetyczna układu. Musisz rozpatrzyć dwa etapy ruchu – zderzenie pierwszej kuli z drugą i zderzenie drugiej kuli z trzecią. Aby wyznaczyć z otrzymanego układu równań szukaną wartość, należy go przekształcić – wyciągnij przed nawiasy masy, pomnóż drugie równanie przez 2 i podziel przekształcone równanie energii przez przekształcone równanie pędu (wykorzystaj wzór skróconego mnożenia: (a2 – b2) = (a – b)(a + b)). Gdy otrzymasz równanie liniowe, wstaw go do układu równań zamiast równania kwadratowego. Dla etapu drugiego postąp analogicznie (uważaj, by brać odpowiednie masy oraz prędkości kul – prędkość drugiej kuli na końcu etapu pierwszego to jej prędkość na początku etapu drugiego).