Dane:
m1 = 300 kg
m2 = 200 kg
h = 4 m
x = 4 cm = 0,04 m
Niech oś układu współrzędnych będzie zwrócona pionowo w dół.
Spadek bijaka jest swobodny, więc zachowana zostaje jego energia mechaniczna:

![]()
Podczas zderzenia niesprężystego zachowany zostaje pęd układu bijak – pal:
![]()

Podczas zderzenia niesprężystego nie zostaje zachowana energia układu – po zderzeniu część energii zostaje zamieniona na pracę wykonywaną podczas pokonywania oporów ruchu:
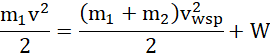
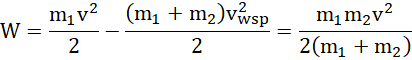
Praca to iloczyn skalarny siły i przemieszczenia (siła ma wartość ujemną, gdyż działa przeciwnie do zwrotu osi):
![]()
więc:
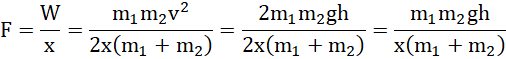

![]()
Odpowiedź: Średnia siła oporów ruchu podczas zagłębiania się pala wyniosła około 118 kJ.

Na początek oblicz prędkość bijaka zaraz przed uderzeniem o pal: skorzystaj z zasady zachowania energii i zapisz równość pomiędzy energią początkową (energia potencjalna) i końcową (kinetyczna). Następnie wylicz prędkość pala i bijaka po zderzeniu – z zasady zachowania pędu pęd przed uderzeniem (pęd bijaka) jest równy pędowi po zderzeniu (pęd bijaka wraz z palem – suma mas pomnożona przez prędkość wspólną). W przypadku zderzenia niesprężystego energia układu nie zostanie zachowana – po zderzeniu część energii zostanie zamieniona na pracę pokonującą opory ruchu. Wartość pracy obliczysz, odejmując od energii początkowej, energię kinetyczną układu po zderzeniu. Na koniec wyznacz wartość siły – jest to iloraz pracy i przemieszczenia x (zwróć uwagę, zwrot wektora siły jest niezgodny ze zwrotem osi układu współrzędnych, ale kąt pomiędzy wektorem siły i przemieszczenia wynosi 180 stopni, więc znakiem iloczynu i tak będzie plus). Wstaw do równości wyznaczoną pracę oraz prędkość i wylicz wartość szukanej siły.