Oblicz różnicę pomiędzy energią kinetyczną kul przed i po zderzeniu, wiedząc, że kule o masach m1 = 2 kg i m2 = 4 kg poruszają się naprzeciwko siebie z prędkościami v1 = 2 
Dane:
m1 = 2 kg
m2 = 4 kg
v1 = 2 
v2 = 4
Podczas zderzenia niesprężystego zachowany zostaje pęd układu, ale energia kinetyczna kul zostaje pomniejszona o wartość energii wewnętrznej wytworzonej podczas zderzenia.
Wyliczmy prędkość wspólną kul po złączeniu się:
Niech oś układu współrzędnych będzie zwrócona zgodnie z kierunkiem ruchu drugiej (cięższej) kuli sprzed zderzenia.
Z zasady zachowania pędu:
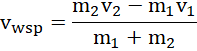
Równość energii można zapisać:
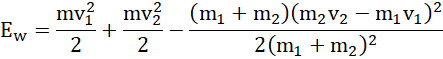
Co po sprowadzeniu do wspólnego mianownika i zredukowaniu składników daje:
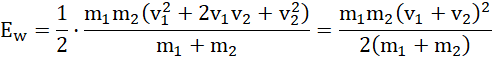
Odpowiedź: Po zderzeniu kul zmiana energii kinetycznej wyniosła 24 J.
Pamiętaj, podczas zderzenia niesprężystego pęd układu zostaje zachowany, ale część energii kinetycznej kul sprzed zderzenia ulega zamianie w ich energię wewnętrzną. Z równania pędu wyznacz prędkość wspólną po zderzeniu (zwróć uwagę, zwroty wektorów prędkości kul są przeciwne, prędkość niezgodna ze zwrotem osi musi zostać wzięta ze znakiem minus). Suma energii kinetycznych kul sprzed zderzenia to suma energii kinetycznej połączonych kul i energii wewnętrznej (równej zmianie energii w czasie zderzenia). Wstaw wyznaczoną wcześniej prędkość wspólną i przekształć równość, aby poznać wartość energii wewnętrznej.