Oblicz prędkość sprzed zderzenia sprężystego i masę mniejszej kulki, wiedząc, że dwie kule zostały zawieszone na równoległych niciach o długości l = 0,2 m, mniejszą z nich odchylono o 90 stopni i puszczono swobodnie, a po zderzeniu się kulą o masie m₂ = 0,06 kg, każda z nich wzniosła się na taką samą wysokość.

Dane:

α = 90°

l = 0,2 m

m₂ = 0,06 kg

Niech zwrot osi układu współrzędnych będzie zgodny z kierunkiem ruchu mniejszej kuli przed zderzeniem.

W przypadku zderzenia sprężystego, po zderzeniu zostają zachowany pęd i energia mechaniczna układu.

Z zasady zachowania energii dla mniejszej kuli:

$\text{[math]}$

$\text{[math]}$ , gdzie v₁ – prędkość mniejszej kuli w położeniu równowagi przed zderzeniem

$\text{[math]}$

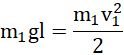
W analogiczny sposób możemy wyznaczyć prędkości kul po zderzeniu:

$\text{[math]}$

gdzie h to wysokość, na jaką wzniosły się kule po zderzeniu.

Z zasady zachowania pędu:

$\text{[math]}$

Zwroty wektorów prędkości nie są zgodne, więc:

$\text{[math]}$

wstawiając wyznaczone prędkości po zderzeniu:

$\text{[math]}$

Wykorzystując zasadę zachowania pędu oraz zasadę zachowania energii zapiszmy:

$\text{[math]}$

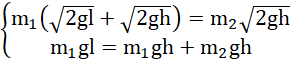
z niego wyznaczamy:

$\text{[math]}$

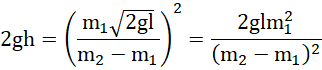
oraz:

$\text{[math]}$

po przyrównaniu do siebie wyrażeń i zredukowaniu wyrazów:

$\text{[math]}$

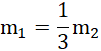
Odpowiedź: Mniejsza kulka przed zderzeniem osiągnęła prędkość 2 $\text{[math]}$ , a jej masa to 0,02 kg.

Na początek zastosuj zasadę zachowania energii mechanicznej dla mniejszej kulki – na początku jej energia mechaniczna to energia potencjalna, a zaraz przed zderzeniem – energia kinetyczna. Z otrzymanej równości wyznacz prędkość kulki. Wykorzystaj tę zasadę jeszcze raz i postępując identycznie, wyznacz prędkości kul po zderzeniu (teraz wysokość potrzebna do wzoru na energię potencjalną to pewna wartość h, co ważne, taka sama dla każdej z kul, gdyż wznoszą się one na taką samą wysokość po zderzeniu). Teraz skorzystaj z zasady zachowania pędu, pęd początkowy to pęd mniejszej kuli, a pęd końcowy to suma pędu każdej z kul po zderzeniu. Zwróć uwagę na zwrot wektora prędkości każdej z kul – pierwsza po zderzeniu zmieni zwrot, a druga będzie poruszać się tak, jak pierwsza przed zderzeniem – umieść przed składnikiem znak minus, gdy zwrot nie zgadza się ze zwrotem ustalonej na początku zadania osi. Do układu równań przydatna będzie jeszcze równość wynikająca z zasady zachowania energii dla układu dwóch kul – energia początkowa to energia potencjalna mniejszej kuli, a energia końcowa – energia potencjalna każdej z kul po zderzeniu (obie osiągnęły wysokość h). Z równań wyznacz wartość h i przyrównaj je do siebie, po przekształceniach i redukcji otrzymasz zależność pomiędzy masami kul.