Oblicz prędkość oraz energię kinetyczną kulki o masie m = 10 g w momencie przechodzenia przez najniższe możliwe położenie, wiedząc, że kulka została zaczepiona na nici o długości l = 40 cm oraz została odchylona od pionu o α = 60°, a przyspieszenie ziemskie przyjęto jako g = 10 
Dane:
m = 10 g = 0,01 kg
l = 40 cm = 0,4 m
α = 60°
g = 10 
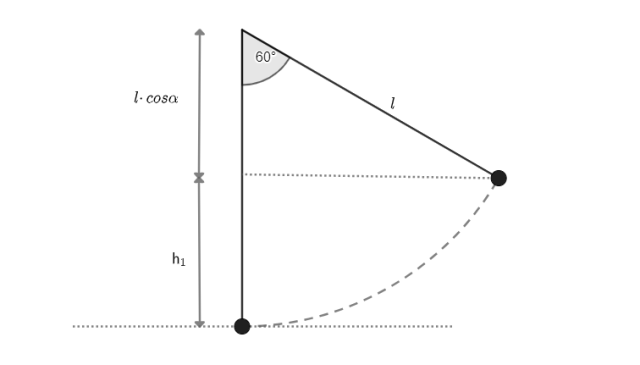
Za poziom odniesienia przyjmijmy najniższe możliwe położenie kulki.
Przyjmijmy, że na kulkę nie działają opory ruchu, wtedy nic nie spowalnia kulki,
więc z zasady zachowania energii:
W momencie wychylenia energia mechaniczna kulki jest równa jej energii potencjalnej:
W najniższym położeniu energia kinetyczna kulki jest równa energii kinetycznej:
czyli:
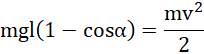
Odpowiedź: Maksymalna prędkość kulki wyniosła 
Prędkość kulki będzie maksymalna, gdy żadne opory ruchu nie będą jej spowalniać. Jednocześnie pomijając siły zewnętrzne możesz skorzystać z zasady zachowania energii mechanicznej – jej wartość w każdym momencie ruchu jest taka sama. Gdy kulka jest wychylona, jej energia mechaniczna jest równa energii potencjalnej – wysokość kulki wyznacz, wykorzystując zależności trygonometryczne (w ten sposób obliczysz, długość nitki, która znajduje się ponad kulką, wysokość od podłoża otrzymasz, odejmując od długości całej nitki, tę wartość). W najniższym położeniu energia potencjalna wynosi zero (gdyż przyjęliśmy tutaj punkt odniesienia), więc cała energia mechaniczna to energia kinetyczna kulki. Z otrzymanej równości wyznacz i wylicz prędkość ciała.