Oblicz średnią wartość siły zderzenia, wiedząc, że piłka o masie mp = 57 g leciała poziomo z prędkością vp = 36 
Dane:
mp = 57 g = 0,057 kg
vp = 36 
t = 1,5 ms = 0,0015 s
α = 60°
Niech oś układu współrzędnych będzie miała kierunek poziomy, a ściana będzie do niej prostopadła.
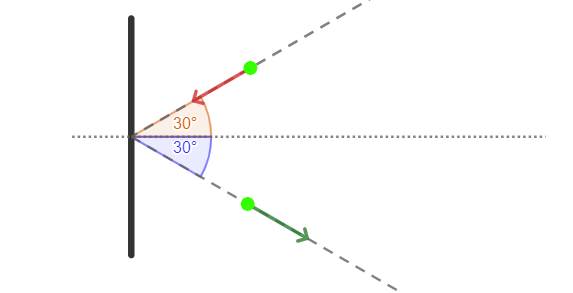
Piłka uderza o ścianę sprężyście, czyli zostaje zachowany jej pęd:
Wzdłuż osi x zwrot wektora prędkości piłki przed i po uderzenie zmienił się, więc:
Z uogólnionej postaci drugiej zasady dynamiki:
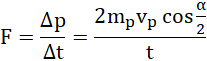
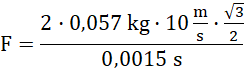
Odpowiedź:
Zauważ, skoro kąt pomiędzy wektorami prędkości piłki wyniósł 60 stopni, to uderzyła ona w ścianę pod kątem 30 stopni do poziomu (zderzenie jest sprężyste, nie dochodzi do żadnych odkształceń). Ze względy na sprężystość zderzenia, pęd piłki zostaje zachowany. Ze względu na fakt, że wektor prędkości po uderzeniu zmienił swój zwrot wzdłuż osi x, przyrost pędu to dwukrotność pędu na początku badania. Średnią wartość siły wyliczysz, stosując uogólnioną postać drugiej zasady dynamiki: średnia siła to iloraz przyrostu pędu i przyrostu czasu.