Dane:
m1 = m
m2 = 9m
v01
Niech zwrot osi układu współrzędnych będzie zgodny z kierunkiem ruchu kuli przed zderzeniem.
W przypadku zderzenia doskonale sprężystego po zderzeniu zostaje zachowany pęd i energia kinetyczna kul.
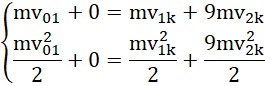
po podzieleniu przez masę oraz pomnożeniu drugiej równości przez 2:
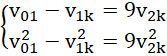
po podzieleniu drugiego równania przez pierwsze:
![]()
co po wstawieniu do pierwszej równości daje:
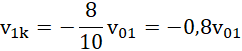
oraz:
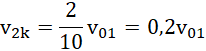
Odpowiedź: Pierwsza kula porusza się z prędkością ![]()
![]()

Pamiętaj, podczas zderzenia doskonale sprężystego zostaje zachowany pęd oraz energia kinetyczna układu. Zapisując równość pędów, zwróć uwagę, wektory prędkości kul są zgodne, więc składniki należy wziąć ze znakiem plus. Aby wyznaczyć z otrzymanego układu równań szukane prędkości, należy go przekształcić – najpierw skróć w równaniach masę i pomnóż drugie z nich przez 2, następnie podziel przekształcone równanie energii przez przekształcone równanie pędu (wykorzystaj wzór skróconego mnożenia: (a2 – b2) = (a – b)(a + b)). Gdy otrzymasz równanie liniowe, wstaw go do układu równań zamiast równania kwadratowego. Znak otrzymanego wyniku oznacza zwrot wektora prędkości kuli – znak minus oznacza zwrot przeciwny do ustalonego zwrotu osi układu współrzędnych, a znak plus – zwrot zgodny.