Oblicz wartość pracy potrzebnej do wciągnięcia ruchem jednostajnym wagonika o masie m = 250 kg na odległość l = 25 m, wiedząc, że wysokość góry to h = 5 m, a współczynnik tarcia wynosi f = 0,05.

Dane:

l = 25 m

h = 5 m

f = 0,05

m = 250 kg

Niech oś x będzie miała kierunek równoległy do wzniesienia i będzie zwrócona zgodnie z kierunkiem ruchu wagonika, a oś y będzie do niej prostopadła, zwrócona do góry.

Niech α – kąt nachylenia góry

Wykorzystując twierdzenie Pitagorasa i zależności trygonometryczne:

$\text{[math]}$

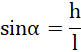
Na wagonik działa siła ciężkości, siła reakcji podłoża, siła tarcia oraz siła, z jaką wagonik jest wciągany.

Rozłóżmy siłę ciężkości na składowe:

$\text{[math]}$

Ponadto:

$\text{[math]}$

Siła reakcji podłoża oraz składowa $\text{[math]}$ równoważą się.

Wagonik porusza się ruchem jednostajnym, więc wypadkowa pozostałych sił jest równa zero:

$\text{[math]}$

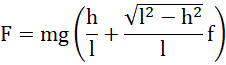
Praca to iloczyn skalarny siły i przesunięcia:

$\text{[math]}$

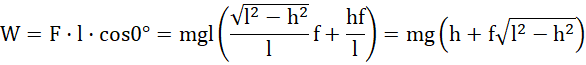
Odpowiedź: Wciągarka wykonała pracę o wartości około 15,3 kJ.

Zastanów się, jakie siły działają na wagonik, są to: siła ciężkości (rozłóż ją na składową równoległą i prostopadłą do wzgórza), siła reakcji podłoża (zwrócona prostopadle do zbocza w górę), siła tarcia (zwrócona przeciwnie do ruchu wagonika) i siła, z jaką wciągano wagonik (zwrócona zgodnie z kierunkiem ruchu wagonika). Siła reakcji podłoża i składowa prostopadła siły ciężkości równoważą, się, więc, aby wagonik poruszał się jednostajnie, wypadkowa sił równoległych do zbocza musi wynieść zero. Zwróć uwagę na znak każdej z sił – siły zwrócone przeciwnie do ruchu wagonika (taki zwrot osi przyjęliśmy) należy wziąć ze znakiem minus. W miejsce funkcji trygonometrycznych wstaw stosunki odpowiednich boków trójkąta prostokątnego (jest to przekrój góry), a następnie wyznacz szukaną siłę wciągającą wagonik. Na koniec wylicz pracę, jest to iloczyn siły wciągającej, przesunięcia (długości zbocza) i cosinusa 0 stopni (zwrot siły pokrywa się z ruchem wagonika).