Wykonaj konieczne obliczenia i podaj minimalny współczynnik tarcia, przy którym pudełko nie spadnie z podestu, wiedząc, że jest ono ustawione l = 45 cm od brzegu podestu, masa pudełka wynosi M = 40 g, masa śrutu to m = 1 g, pocisk leciał z prędkością v0 = 120 
Dane:
M = 40 g = 0,04 kg
m = 1 g = 0,001 kg
v0 = 120 
vk = 
l = 45 cm = 0,45 m
Z wcześniejszego Podpunkt:u:
Zbadajmy przypadek graniczny, czyli taki, w którym współczynnik tarcia jest możliwie najmniejszy – dla każdej większej wartości pudełko zatrzyma się przed krawędzią.
Na pudełko działa niezrównoważona siła tarcia, więc z drugiej zasady dynamiki porusza się ono ruchem jednostajnie opóźnionym:
ponadto:
czyli:
Czas trwania ruchu wyznaczamy z:
Drogę w ruchu jednostajnie opóźnionym z prędkością początkową zapisujemy jako:
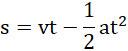
Co razem daje:
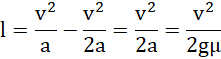
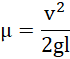
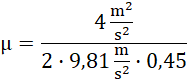
Pudełko zatrzyma się na brzegu podestu, gdy współczynnik tarcia wyniesie 0,45.
Oznacza to, że pudełko nie spadnie, gdy 
Zbadaj przypadek, gdy pudełko znajdzie się możliwie najbliżej brzegu podestu i z niego nie spadnie, dla każdej wartości współczynnika większej od tej, pudełko pozostanie na podeście. Wykorzystaj prędkość pudełka z wcześniejszego Podpunkt:u. Na pudełko działa siła tarcia, więc wypadkowa sił nie jest zerowa, co z drugiej zasady dynamiki daje, że porusza się ono ruchem jednostajnie zmiennym (tutaj opóźnionym). Siła tarcia to więc iloczyn masy i przyspieszenia, ale także iloczyn masy, przyspieszenia ziemskiego i współczynnika tarcia. Z otrzymanej równości wyznacz wartość przyspieszenia. Następnie posłuż się wzorami opisującymi prędkość i drogę w ruchu jednostajnie zmiennym z prędkością początkową. Ze wzoru na prędkość wyznacz czas i wstaw go do drugiego wyrażenia. Z otrzymanej równości wyznacz współczynnik tarcia.