Zbiór zadań, Wydawnictwo: WSiP

Zadanie 4.13, c) - strona 26

Wyznacz funkcję pracy od czasu oraz mocy chwilowej od czasu, wiedząc, że silnik rozpędza platformę o masie 500 kg, której promień ma długość 1,5 m, w taki sposób, że po czasie 10 sekund od rozpoczęcia ruchu częstotliwość obrotów osiąga wartość 1,5 Hz.

Wyznaczamy pracę jako funkcję czasu:

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

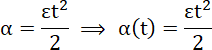
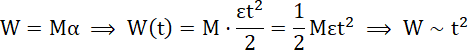
Praca w zależności od czasu jest funkcją kwadratową.

Wyznaczamy moc jako funkcję czasu:

$\text{[math]}$

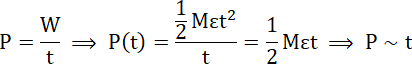
Moc w zależności od czasu jest funkcją liniową.

Pracę $\text{[math]}$ możemy wyrazić jako $\text{[math]}$ . Ponieważ działająca siła $\text{[math]}$ ma stałą wartość oraz ramię siły $\text{[math]}$ także się nie zmienia w czasie, to moment siły $\text{[math]}$ jest stały w czasie. Zmianie natomiast ulega kąt obrotu $\text{[math]}$ . Na podstawie wyliczeń z podpunktu b) wiadomo, że można go wyrazić w postaci $\text{[math]}$ . W takim razie praca jest wprost proporcjonalna do kwadratu czasu.

Z kolei moc $\text{[math]}$ opisuje wyrażenie $\text{[math]}$ . Dochodzi do skrócenia jednego czasu $\text{[math]}$ w tym wyrażeniu, więc moc jest wprost proporcjonalna do czasu.

Zadanie 9, strona 78, Fizyka. Klasa 7. Podręcznik - rozwiązania i odpowiedzi

Zadanie 8., strona 31, Fizyka z plusem. Klasa 8. Podręcznik - rozwiązania i odpowiedzi

Zadanie 31.2., strona 114, Zbiór zadań z fizyki dla szkoły podstawowej. Klasa 7-8 - rozwiązania i odpowiedzi

Zadanie 10.2, strona 61, Fizyka. Klasa 4. Zakres rozszerzony. Zbiór zadań - rozwiązania i odpowiedzi

Zadanie 13, strona 109, Fizyka. Klasy 1-3. Zakres podstawowy. Zbiór zadań - rozwiązania i odpowiedzi

Zadanie 4., strona 111, Fizyka. Klasa 7. Podręcznik - rozwiązania i odpowiedzi

Zadanie 6.5., strona 266, Zrozumieć fizykę. Klasa 1. Zakres rozszerzony. Zbiór zadań - rozwiązania i odpowiedzi

Zadanie 5.3.7., strona 183, Zrozumieć fizykę. Klasa 1. Zakres rozszerzony. Zbiór zadań - rozwiązania i odpowiedzi

Zadanie To powinieneś umieć 9., strona 55, Odkryć fizykę. Klasa 3. Zakres podstawowy. Podręcznik - rozwiązania i odpowiedzi

Zadanie 1.1.8., strona 14, Zrozumieć fizykę. Klasa 1. Zakres rozszerzony. Zbiór zadań - rozwiązania i odpowiedzi

18

18

18

Zadanie 1.4

19

19

19

19

19

19

19

Zadanie 1.5

19

19

19

19

19

19

Zadanie 1.6

19

19

19

19

19

20

20

20

20

Zadanie 2.7

21

21

21

21

Zadanie 3.1

21

21

21

21

Zadanie 3.2

22

22

22

22

Zadanie 3.3

22

22

22

22

22

Zadanie 3.5

22

22

22

23

23

23

Zadanie 3.9

23

23

23

23

Zadanie 3.11

23

23

23

23

24

24

24

24

24

25

Zadanie 4.7

25

25

25

Zadanie 4.8

25

25

25

25

25

25

Zadanie 4.10

25

25

25

25

Zadanie 4.11

26

26

26

26

26

Zadanie 4.13

26

26

26

26

26

Zadanie 5.1

27

27

27

27

Zadanie 5.3

27

27

27

Zadanie 5.4

27

27

27

28

Zadanie 5.6

28

28

28

28

Zadanie 5.7

28

28

28

Zadanie 5.8

29

29

29

Zadanie 5.9

29

29

29

Zadanie 5.10

29

29

29

29

29

Zadanie 5.13

30

30

30

30

30

Zadanie 6.2

30

30

30

30

30

Zadanie 6.5

31

31

31

Zadanie 6.6

31

31

31

Zadanie 6.7

31

31

31

Zadanie 6.8

31

31

31

31

31

Zadanie 6.9

32

32

32

32

32

32

33

33

Zadanie 8.1

33

33

33

34

Zadanie 8.3

34

34

34

34

34

Zadanie 8.5

34

34

34

34

34

34

35

Zadanie 8.8

35

35

35

Zadanie 8.9

35

35

35

Pełny spis treści