Udowodnij, że współczynnik tarcia statycznego między kulą a ścianą musi mieć wartość co najmniej 1, aby, kula o masie
, której promień ma długość
, że została zawieszona na linie, w taki sposób, że styka się ze ścianą (rysunek).
TEZA:
DOWÓD:
I zasada dynamiki dla ruchu obrotowego:
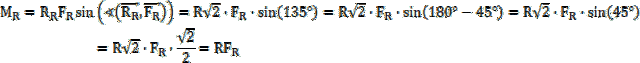
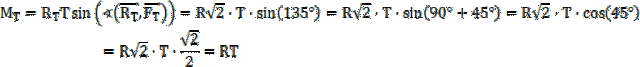
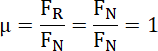
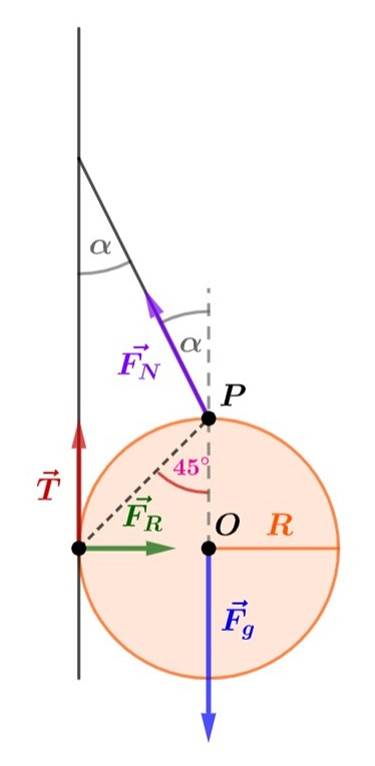
Zauważ, że skoro kula pozostaje w spoczynku, to zgodnie z pierwszą zasadą dynamiki dla ruchu obrotowego, wypadkowy moment sił
jest równy zeru. Obierz oś obrotu w punkcie
, a następnie wyznacz moment każdej z sił, używając wzoru na moment siły
, gdzie
– ramię siły (wektor odległości punktu przyłożenia siły od osi),
– wartość przyłożonej siły,
– kąt zawarty między wektorami
.
Stąd wynika, że moment siły ciężkości
oraz moment siły naciągu liny
są zerowe. Zauważ, że z reguły prawej dłoni wynika, że ich momenty sił tarcia oraz reakcji podłoża są przeciwnie zwrócone (tę zasadę obrazuje ilustracja). Stąd wypadkowy moment sił jest równy ich różnicy, czyli moment siły tarcia
oraz moment siły reakcji ściany
są sobie równe. Z otrzymanego równania wyznacz wartość współczynnika tarcia statycznego,
wiedząc, że zachodzi relacja
. Jest to minimalna wartość współczynnika, więc aby nie doszło do poślizgu, to jego wartość nie może być mniejsza.
Zgodnie z zasadami dynamiki siła reakcji podłoża równoważy siłę nacisku
.
