DANE:
SZUKANE:
WZÓR:
Na drabinę działają siły: ciężkości
, reakcji podłoża
, reakcji ściany
oraz tarcia
.
Wyznaczamy wszystkie siły:
I zasada dynamiki:
I zasada dynamiki dla ruchu obrotowego:
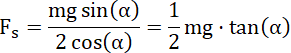
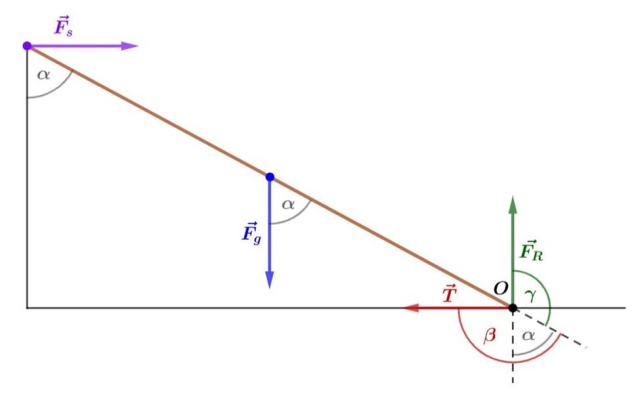
Na rysunku zostały przedstawione siły działające na drabinę.
Zauważ, że skoro drabina pozostaje w spoczynku, to zgodnie z pierwszą zasadą dynamiki wypadkowa działających sił jest równa zeru. W takim razie siła grawitacji równoważy się z siłą reakcji podłoża, a siła tarcia statycznego z siłą reakcji ściany.
Następnie przeanalizuj ruch obrotowy – zastosuj I zasadę dynamiki, która mówi, że wypadkowy moment sił jest zerowy. Obierz oś obrotu w punkcie styku drabiny z podłożem, a następnie wyznacz moment każdej z sił, używając wzoru na moment siły
, gdzie
– ramię siły (wektor odległości punktu przyłożenia siły od osi),
– wartość przyłożonej siły,
– kąt zawarty między wektorami
.
W tym przypadku tarcie i siła reakcji podłoża są równe zeru, ponieważ są przyłożone do punktu osi obrotu.
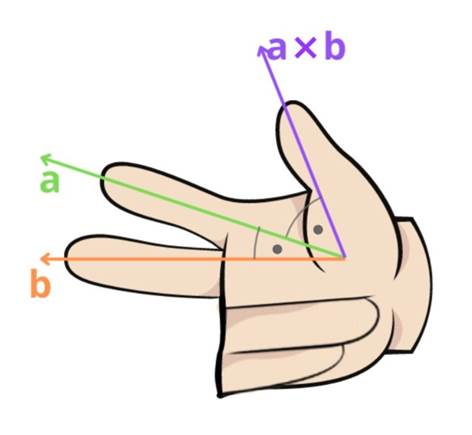
Zauważ, że z reguły prawej dłoni wynika, że ich momenty sił są przeciwnie zwrócone (tę zasadę obrazuje ilustracja). Stąd wypadkowy moment sił jest równy ich różnicy, czyli moment siły ciężkości
oraz moment siły reakcji ściany
są sobie równe. Z otrzymanego równania wyznacz wartość siły
.
