DANE:
![]()
![]()
![]()
![]()
![]()
SZUKANE:
![]()
![]()
WZÓR:
Wyznaczamy przyspieszenie kuli:
![]()
![]()
![]()
![]()
![]()
![]()
![]() (I zasada dynamiki)
(I zasada dynamiki)
![]()
![]()
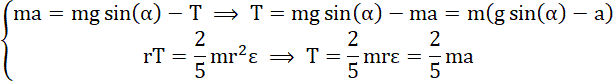
![]()
![]()
![]()
Wyznaczamy siłę tarcia:
![]()
![]()

Potraktuj kulę jako jednorodną bryłę, więc jej moment bezwładności względem osi obrotu (symetrii) wynosi odpowiednio
![]() .
.
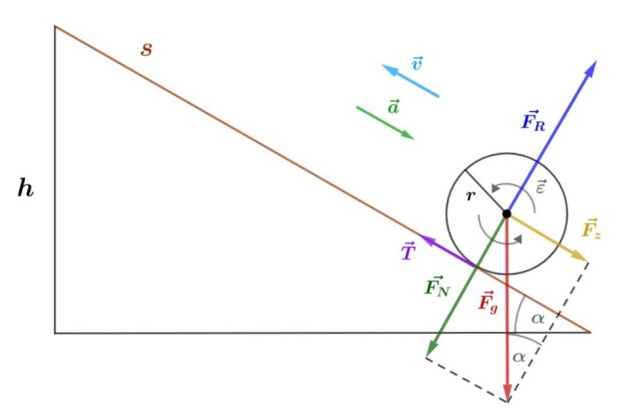
Najpierw dokonaj rozkładu sił, a następnie utwórz układ równań dotyczący ruchu postępowego bryły. Skorzystaj z drugiej zasady dynamiki. Zauważ, że siła nacisku
![]() i reakcji podłoża
i reakcji podłoża
![]() równoważą się, więc siła wypadkowa
równoważą się, więc siła wypadkowa
![]() jest zależna od siły zsuwającej
jest zależna od siły zsuwającej
![]() i tarcia
i tarcia
![]() .
.
Skoro rura się zsuwa w dół, to siła tarcia jako siła hamująca ruch jest skierowana w przeciwną stronę, czyli jest zwrócona w górę równi, aby zapobiec zsuwaniu się kuli w dół równi.
Ze względu na to, że tarcie powoduje ruch kuli w „górę”, a siła zsuwająca w „dół”, to wypadkowa jest różnicą wartości tych sił.
Następnie przeanalizuj ruch obrotowy krążka, korzystając ze wzorów wiążących wypadkowy moment siły
![]() (oblicz go ze wzoru
(oblicz go ze wzoru
![]() , gdzie
, gdzie
![]() – ramię siły (wektor odległość punktu przyłożenia siły od osi obrotu),
– ramię siły (wektor odległość punktu przyłożenia siły od osi obrotu),
![]() – wartość przyłożonej siły (w tym przypadku tarcie),
– wartość przyłożonej siły (w tym przypadku tarcie),
![]() – kąt zawarty między wektorami
– kąt zawarty między wektorami
![]() ) z momentem bezwładności rury
) z momentem bezwładności rury
![]() oraz przyspieszenia kątowego
oraz przyspieszenia kątowego
![]() (
(
![]() ). Użyj także zależności
). Użyj także zależności
![]() , aby wyznaczyć przyspieszenie liniowe
, aby wyznaczyć przyspieszenie liniowe
![]() .
.