DANE:
SZUKANE:
WZÓR:
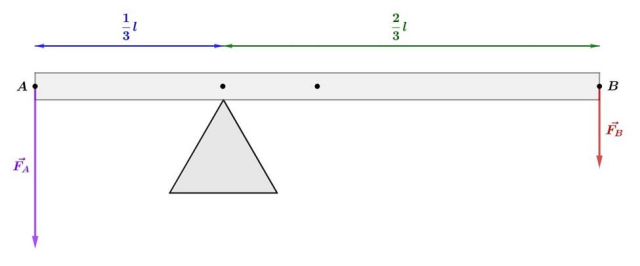
Sytuacja I:
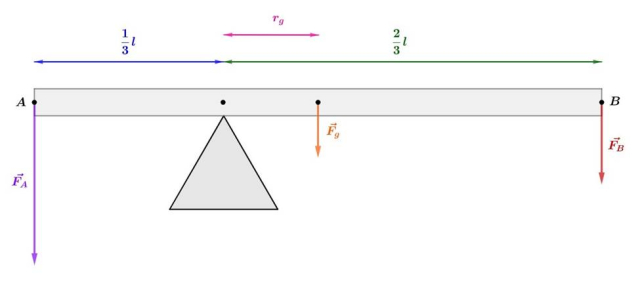
Sytuacja II:
Sytuacja I:
Aby dźwignia dwustronna pozostawała w równowadze, to wypadkowy moment sił działających na nią musi być równy zeru.
Wyznacz moment każdej z sił, używając wzoru na moment siły
, gdzie
– ramię siły (wektor odległości punktu przyłożenia siły od osi),
– wartość przyłożonej siły,
– kąt zawarty między wektorami
.
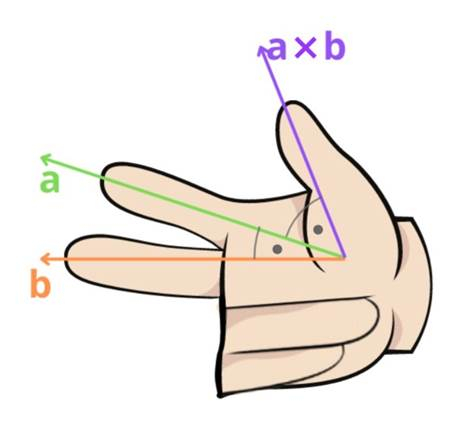
Zauważ, że z reguły prawej dłoni wynika, że moment siły
jest przeciwny do momentu siły
(tę zasadę obrazuje ilustracja). Stąd wypadkowy moment sił
jest równy różnicy momentów
oraz
, czyli te momenty są sobie równe. Z otrzymanego równania wyznacz wartość siły przyłożonej w punkcie B.
Sytuacja I:
Aby dźwignia dwustronna pozostawała w równowadze, to wypadkowy moment sił działających na nią musi być równy zeru.
Wyznacz moment każdej z sił, używając wzoru na moment siły
, gdzie
– ramię siły (wektor odległości punktu przyłożenia siły od osi),
– wartość przyłożonej siły,
– kąt zawarty między wektorami
.
Zauważ, że z reguły prawej dłoni wynika, że moment siły
jest przeciwny do momentów sił
oraz
(tę zasadę obrazuje ilustracja). Stąd wypadkowy moment sił
jest równy różnicy tych momentów sił, czyli moment siły
jest równy różnicy
i
. Z otrzymanego równania wyznacz wartość siły przyłożonej w punkcie B.
