Masz udowodnić, że dla pary prostych 𝑎 i 𝑏, które są skośne, istnieje tylko jedna para płaszczyzn 𝛼 i 𝛽, w których𝑎 zawiera się w 𝛼, 𝑏 zawiera się w 𝛽 i płaszczyzna 𝛼 jest równoległa do płaszczyzny 𝛽.
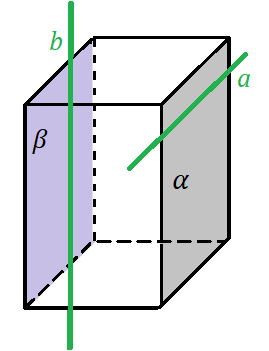
Prowadząc przez prostą 𝑎 płaszczyznę 𝛼 okaże się, że jeśli utworzymy prostą 𝑏 skośną do prostej 𝑎, to jest tyko jedna płaszczyzna 𝛽, która będzie zawierała prostą 𝑏 i będzie jednocześnie równoległa do płaszczyzny 𝛼.

Aby ułatwić sobie wyobrażenie tych przestrzeni i prostych, zbuduj je na prostopadłościanie. Spójrz na rysunek. Każda inna utworzona płaszczyzna 𝛽 nie będzie równoległa do płaszczyzny 𝛼.

Zadanie 1.8.
16Zadanie 1.11.
17Zadanie 1.13.
17Zadanie Prosto do matury 5.
18Zadanie 2.1.
24Zadanie 2.5.
24Zadanie 2.8.
25Zadanie 2.9.
25Zadanie 2.11.
25Zadanie 2.12.
25Zadanie 2.13.
26Zadanie 2.14.
26Zadanie 2.15.
26Zadanie 3.1.
30Zadanie 3.2.
31Zadanie 3.3.
31Zadanie Prosto do matury 5.
33Zadanie 4.1.
42Zadanie 4.3.
42Zadanie 4.6.
42Zadanie 4.7.
42Zadanie 4.11.
42Zadanie 4.14.
43Zadanie 4.17.
43Zadanie 5.1.
56Zadanie 5.2.
56Zadanie 5.3.
56Zadanie 5.6.
56Zadanie 5.10.
57Zadanie 5.17.
57Zadanie 5.23.
58Zadanie 6.2.
69Zadanie 6.3.
69Zadanie 6.4.
69Zadanie 6.7.
69Zadanie 6.11.
69Zadanie 6.12.
69Zadanie 7.10.
82Zadanie 37.
90
