Oblicz objętość i pole powierzchni całkowitej walca, którego wysokość wynosi 7, a przekątna przekroju osiowego jest nachylona do płaszczyzny pod kątem 68º. Wyniki podaj, zaokrąglając je do pierwszego miejsca po przecinku.
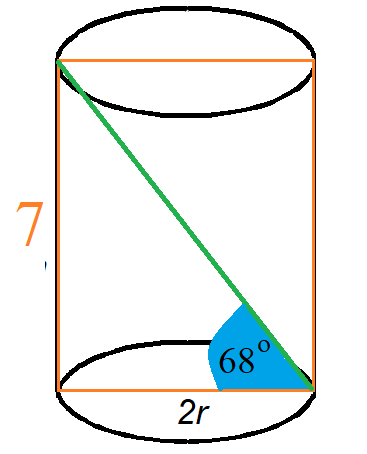
Promień walca:
![]()
![]()
Objętość walca:
![]()
Pole powierzchni całkowitej:
![]()

Rozwiązujesz równania zgodnie z oznaczeniem na rysunku. Najpierw wyznaczasz promień walca, wykorzystując do tego funkcję tangens. Dzięki temu uzyskasz wielkość, która posłuży do obliczenia objętości walca i jego pola powierzchni bocznej.

Zadanie 1.8.
16Zadanie 1.11.
17Zadanie 1.13.
17Zadanie Prosto do matury 5.
18Zadanie 2.1.
24Zadanie 2.5.
24Zadanie 2.8.
25Zadanie 2.9.
25Zadanie 2.11.
25Zadanie 2.12.
25Zadanie 2.13.
26Zadanie 2.14.
26Zadanie 2.15.
26Zadanie 3.1.
30Zadanie 3.2.
31Zadanie 3.3.
31Zadanie Prosto do matury 5.
33Zadanie 4.1.
42Zadanie 4.3.
42Zadanie 4.6.
42Zadanie 4.7.
42Zadanie 4.11.
42Zadanie 4.14.
43Zadanie 4.17.
43Zadanie 5.1.
56Zadanie 5.2.
56Zadanie 5.3.
56Zadanie 5.6.
56Zadanie 5.10.
57Zadanie 5.17.
57Zadanie 5.23.
58Zadanie 6.2.
69Zadanie 6.3.
69Zadanie 6.4.
69Zadanie 6.7.
69Zadanie 6.11.
69Zadanie 6.12.
69Zadanie 7.10.
82Zadanie 37.
90
