Masz obliczyć pole przekroju, który powstał po przecięciu sześcianu o krawędzi 1 płaszczyzną, która przechodzi przez jego podstawę i jest do niej nachylona pod kątem 𝛼.
Przekątna podstawy:
![]()
Pole przekroju jako pole prostokąta:
![]()
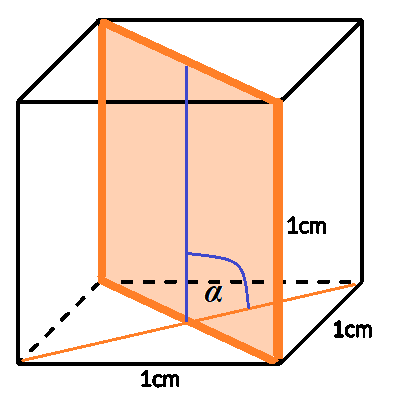
Pole przekroju jako pole trójkąta:
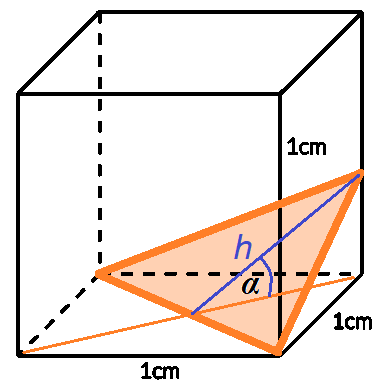
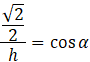
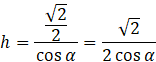
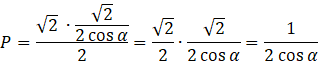
Pole przekroju jako pole trapezu:
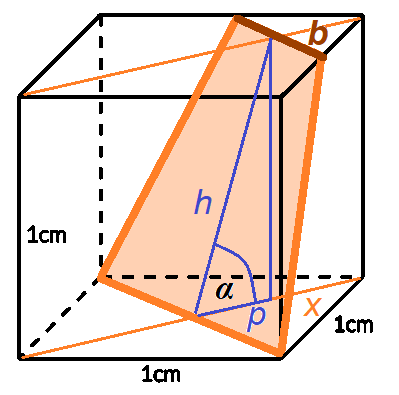
![]()
Wysokość trapezu:
![]()
![]()
Długość ![]()
![]()
![]()
Długości ![]()
![]()
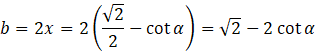
Pole przekroju:
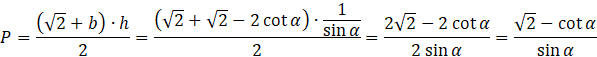

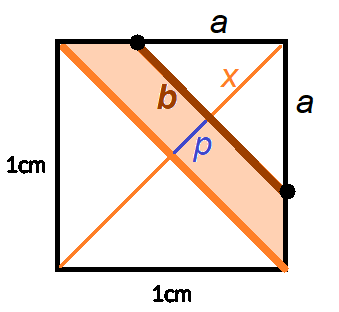
W tej sytuacji masz trzy możliwości, w których będziesz musiał obliczyć pole przekroju które jest: prostokątem lub trójkątem lub trapezem. W pierwszym przypadku pole przekroju to pole prostokąta, którego bokami są przekątna podstawy oraz krawędź boczna sześcianu. W drugim przypadku masz trójkąt o podstawie, która jest przekątną podstawy sześcianu, a jego wysokość można wyznaczyć z funkcji trygonometrycznej. Istnieje również możliwość, że przekrój jest trapezem. Dłuższa podstawa ma długość przekątnej podstawy sześcianu. Jego wysokość możesz wyznaczyć z funkcji trygonometrycznej. Wyznaczenie krótszej podstawy wymaga więcej obliczeń. Na rysunku przedstawiono również widok tego sześcianu z góry. Obliczasz sobie długość ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

Zadanie 1.8.
16Zadanie 1.11.
17Zadanie 1.13.
17Zadanie Prosto do matury 5.
18Zadanie 2.1.
24Zadanie 2.5.
24Zadanie 2.8.
25Zadanie 2.9.
25Zadanie 2.11.
25Zadanie 2.12.
25Zadanie 2.13.
26Zadanie 2.14.
26Zadanie 2.15.
26Zadanie 3.1.
30Zadanie 3.2.
31Zadanie 3.3.
31Zadanie Prosto do matury 5.
33Zadanie 4.1.
42Zadanie 4.3.
42Zadanie 4.6.
42Zadanie 4.7.
42Zadanie 4.11.
42Zadanie 4.14.
43Zadanie 4.17.
43Zadanie 5.1.
56Zadanie 5.2.
56Zadanie 5.3.
56Zadanie 5.6.
56Zadanie 5.10.
57Zadanie 5.17.
57Zadanie 5.23.
58Zadanie 6.2.
69Zadanie 6.3.
69Zadanie 6.4.
69Zadanie 6.7.
69Zadanie 6.11.
69Zadanie 6.12.
69Zadanie 7.10.
82Zadanie 37.
90
