Masz podany prostopadłościan o kwadratowej podstawie, której bok ma długość 5√2, a jego wysokość to 20. Został on przecięty płaszczyzną, którą wyznaczyły wychodzące z jednego wierzchołka przekątna podstawy oraz bocznej ściany W tym zadaniu masz obliczyć objętość brył, na jakie ta płaszczyzna podzieliła podany prostopadłościan.
Objętość całości:
![]()
Objętość ostrosłupa:
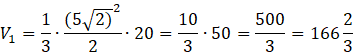
Objętość drugiej figury:
![]()

Wyjaśnienie rozwiązania przedstawiono na rysunku:
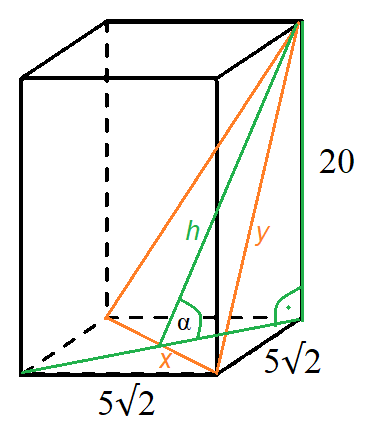
Najpierw obliczasz całą objętość prostopadłościanu. Następnie zauważ, że płaszczyzna podzieliła figurę tak, że jedną z nich jest ostrosłup, którego objętość możesz wyliczyć. Pole podstawy tego ostrosłupa jest równe połowie pola podstawy całego prostopadłościanu. Aby wyznaczyć objętość drugiej figury, od objętości całego prostopadłościanu musisz odjąć obliczoną objętość ostrosłupa.

Zadanie 1.8.
16Zadanie 1.11.
17Zadanie 1.13.
17Zadanie Prosto do matury 5.
18Zadanie 2.1.
24Zadanie 2.5.
24Zadanie 2.8.
25Zadanie 2.9.
25Zadanie 2.11.
25Zadanie 2.12.
25Zadanie 2.13.
26Zadanie 2.14.
26Zadanie 2.15.
26Zadanie 3.1.
30Zadanie 3.2.
31Zadanie 3.3.
31Zadanie Prosto do matury 5.
33Zadanie 4.1.
42Zadanie 4.3.
42Zadanie 4.6.
42Zadanie 4.7.
42Zadanie 4.11.
42Zadanie 4.14.
43Zadanie 4.17.
43Zadanie 5.1.
56Zadanie 5.2.
56Zadanie 5.3.
56Zadanie 5.6.
56Zadanie 5.10.
57Zadanie 5.17.
57Zadanie 5.23.
58Zadanie 6.2.
69Zadanie 6.3.
69Zadanie 6.4.
69Zadanie 6.7.
69Zadanie 6.11.
69Zadanie 6.12.
69Zadanie 7.10.
82Zadanie 37.
90
