Masz podany ostrosłup, w którego podstawie jest romb o boku 16 i kącie ostrym 60º. Jedna z jego krawędzi bocznych przechodzi przez wierzchołek rozwartego kąta rombu i jest prostopadła do płaszczyzny podstawy, natomiast boczne krawędzie tego ostrosłupa, które przechodzą przez wierzchołki kątów ostrych, tworzą kąt 48º. Twoim zadaniem jest wyznaczenie objętości tego ostrosłupa. Wynik zaokrąglij do całości.
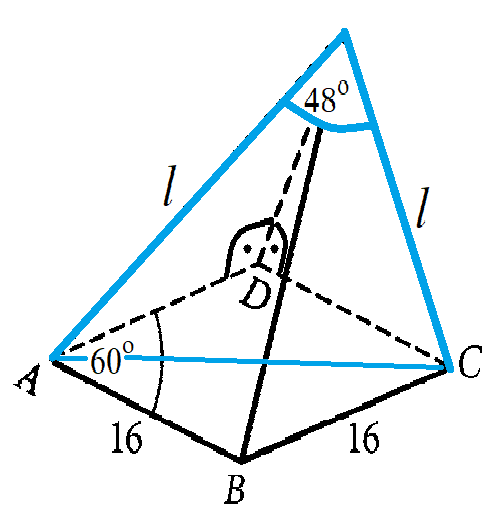
Pole podstawy:
![]()
Wysokość ostrosłupa:
![]()
![]()
![]()
![]()
Objętość ostrosłupa:
![]()

Obliczenia wykonujesz na podstawie rysunku. Pole podstawy obliczasz ze wzoru na pole czworokąta z funkcją sinus. Do wyznaczenia wysokości ostrosłupa wykorzystaj twierdzenie Pitagorasa, a uzyskasz wszystkie dane potrzebne do wyznaczenia objętości.

Zadanie 1.8.
16Zadanie 1.11.
17Zadanie 1.13.
17Zadanie Prosto do matury 5.
18Zadanie 2.1.
24Zadanie 2.5.
24Zadanie 2.8.
25Zadanie 2.9.
25Zadanie 2.11.
25Zadanie 2.12.
25Zadanie 2.13.
26Zadanie 2.14.
26Zadanie 2.15.
26Zadanie 3.1.
30Zadanie 3.2.
31Zadanie 3.3.
31Zadanie Prosto do matury 5.
33Zadanie 4.1.
42Zadanie 4.3.
42Zadanie 4.6.
42Zadanie 4.7.
42Zadanie 4.11.
42Zadanie 4.14.
43Zadanie 4.17.
43Zadanie 5.1.
56Zadanie 5.2.
56Zadanie 5.3.
56Zadanie 5.6.
56Zadanie 5.10.
57Zadanie 5.17.
57Zadanie 5.23.
58Zadanie 6.2.
69Zadanie 6.3.
69Zadanie 6.4.
69Zadanie 6.7.
69Zadanie 6.11.
69Zadanie 6.12.
69Zadanie 7.10.
82Zadanie 37.
90
