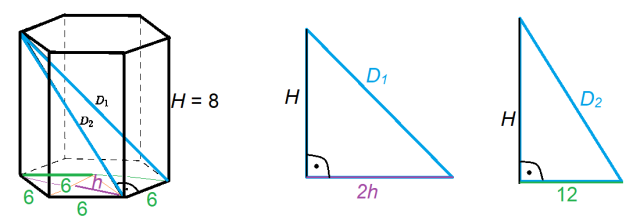
Masz wyznaczyć długości przekątnych graniastosłupa sześciokątnego prawidłowego, którego wysokość wynosi 8, a środek podstawy oddalony jest o 6 od każdego wierzchołka.
![]()
![]()
![]()
![]()
![]()

Zauważ, że możesz tutaj wykorzystać twierdzenie Pitagorasa. Graniastosłup sześciokątny prawidłowy ma w podstawie sześciokąt, który składa się z sześciu trójkątów równobocznych. Znając długość krawędzi podstawy, możesz obliczyć wysokość takiego trójkąta. Ta z kolei posłuży do wyznaczenia jednej z przekątnych. W drugiej z nich wykorzystaj, że podstawa trójkąta to dwukrotna krawędź wcześniej wspomnianego trójkąta równobocznego.

Zadanie 1.8.
16Zadanie 1.11.
17Zadanie 1.13.
17Zadanie Prosto do matury 5.
18Zadanie 2.1.
24Zadanie 2.5.
24Zadanie 2.8.
25Zadanie 2.9.
25Zadanie 2.11.
25Zadanie 2.12.
25Zadanie 2.13.
26Zadanie 2.14.
26Zadanie 2.15.
26Zadanie 3.1.
30Zadanie 3.2.
31Zadanie 3.3.
31Zadanie Prosto do matury 5.
33Zadanie 4.1.
42Zadanie 4.3.
42Zadanie 4.6.
42Zadanie 4.7.
42Zadanie 4.11.
42Zadanie 4.14.
43Zadanie 4.17.
43Zadanie 5.1.
56Zadanie 5.2.
56Zadanie 5.3.
56Zadanie 5.6.
56Zadanie 5.10.
57Zadanie 5.17.
57Zadanie 5.23.
58Zadanie 6.2.
69Zadanie 6.3.
69Zadanie 6.4.
69Zadanie 6.7.
69Zadanie 6.11.
69Zadanie 6.12.
69Zadanie 7.10.
82Zadanie 37.
90
