Masz wyznaczyć objętość i pole powierzchni bocznej ostrosłupa prawidłowego trójkątnego, w którym ściana boczna nachylona jest do podstawy pod kątem 60º, a jego wysokość ma 6√3 cm.
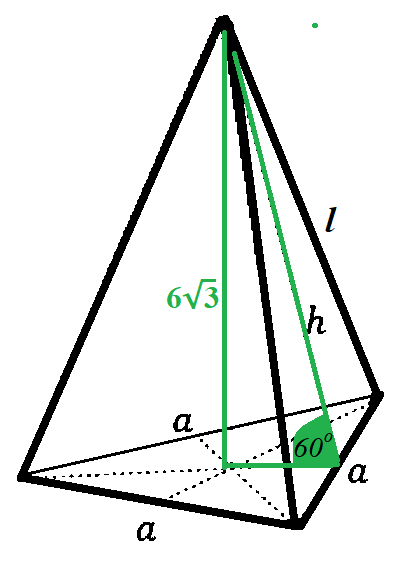
Wysokość ściany bocznej:
![]()
![]()
Długość podstawy trójkąta:
![]()
![]()
Długość krawędzi podstawy:
![]()
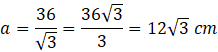
Pole podstawy:
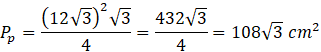
Objętość ostrosłupa:
![]()
Pole powierzchni bocznej:
![]()

Obliczenia wykonujesz na podstawie załączonego rysunku. Wysokość ściany bocznej obliczasz, korzystając z funkcji sinus, natomiast długość podstawy trójkąta z funkcji cosinus. Pole powierzchni bocznej to trzy pola trójkąta, który znajduje się w ścianie bocznej.

Zadanie 1.8.
16Zadanie 1.11.
17Zadanie 1.13.
17Zadanie Prosto do matury 5.
18Zadanie 2.1.
24Zadanie 2.5.
24Zadanie 2.8.
25Zadanie 2.9.
25Zadanie 2.11.
25Zadanie 2.12.
25Zadanie 2.13.
26Zadanie 2.14.
26Zadanie 2.15.
26Zadanie 3.1.
30Zadanie 3.2.
31Zadanie 3.3.
31Zadanie Prosto do matury 5.
33Zadanie 4.1.
42Zadanie 4.3.
42Zadanie 4.6.
42Zadanie 4.7.
42Zadanie 4.11.
42Zadanie 4.14.
43Zadanie 4.17.
43Zadanie 5.1.
56Zadanie 5.2.
56Zadanie 5.3.
56Zadanie 5.6.
56Zadanie 5.10.
57Zadanie 5.17.
57Zadanie 5.23.
58Zadanie 6.2.
69Zadanie 6.3.
69Zadanie 6.4.
69Zadanie 6.7.
69Zadanie 6.11.
69Zadanie 6.12.
69Zadanie 7.10.
82Zadanie 37.
90
