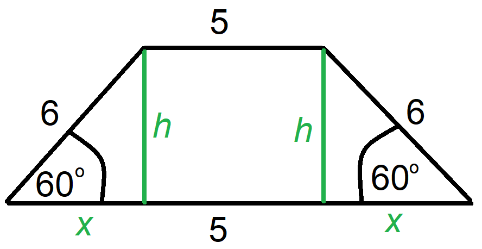
Masz podany przekrój poprzeczny wału ochronnego. Jest on trapezem, którego górna podstawa ma 5 m, a ramiona po 6 m i są one nachylone do dolnej podstawy pod kątem 60º. Masz wyznaczyć dolną szerokość wału oraz obliczyć, ile ziemi należy użyć do usypania takiego wału o długości jednego kilometra. Wynik podaj z dokładnością do jednego metra sześciennego.
Obliczenie wysokości trapezu:
![]()
![]()
Obliczenie długości podstawy trapezu:
![]()
![]()
![]()
Obliczenie objętości potrzebnej ziemi:
![]()

Narysuj sobie przekrój poprzeczny wału i zaznacz podane wartości. Zauważ, że wysokość trapezu oraz fragment jego podstawy jesteś w stanie wyznaczyć z funkcji trygonometrycznych. Dolna podstawa ma długość sumy dwóch szukanych niewiadomych oraz górnej podstawy. Aby obliczyć potrzebną ziemię do wypełnienia wału, musisz obliczyć objętość graniastosłupa, który w podstawie ma trapez równoramienny a jego wysokością będzie długość wspomnianego wału.

Zadanie 1.8.
16Zadanie 1.11.
17Zadanie 1.13.
17Zadanie Prosto do matury 5.
18Zadanie 2.1.
24Zadanie 2.5.
24Zadanie 2.8.
25Zadanie 2.9.
25Zadanie 2.11.
25Zadanie 2.12.
25Zadanie 2.13.
26Zadanie 2.14.
26Zadanie 2.15.
26Zadanie 3.1.
30Zadanie 3.2.
31Zadanie 3.3.
31Zadanie Prosto do matury 5.
33Zadanie 4.1.
42Zadanie 4.3.
42Zadanie 4.6.
42Zadanie 4.7.
42Zadanie 4.11.
42Zadanie 4.14.
43Zadanie 4.17.
43Zadanie 5.1.
56Zadanie 5.2.
56Zadanie 5.3.
56Zadanie 5.6.
56Zadanie 5.10.
57Zadanie 5.17.
57Zadanie 5.23.
58Zadanie 6.2.
69Zadanie 6.3.
69Zadanie 6.4.
69Zadanie 6.7.
69Zadanie 6.11.
69Zadanie 6.12.
69Zadanie 7.10.
82Zadanie 37.
90
