Ściany francuskiej piramidy wykonane są z 603 szklanych tafli w kształcie rombu oraz z 70 tafli, w kształcie trójkąta. Wysokość piramidy to 21,65 m, natomiast długość boku jej podstawy to 35,42 m. Masz wyznaczyć długość bocznej krawędzi, zaokrąglając wynik do jednego miejsca po przecinku.
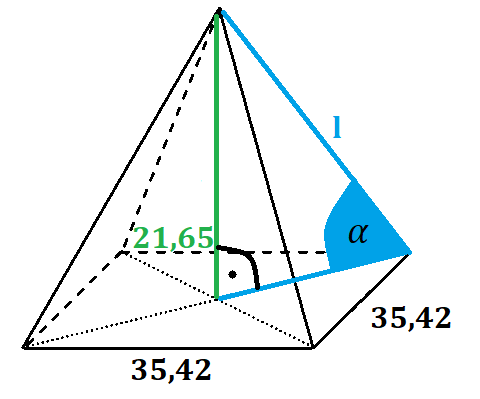
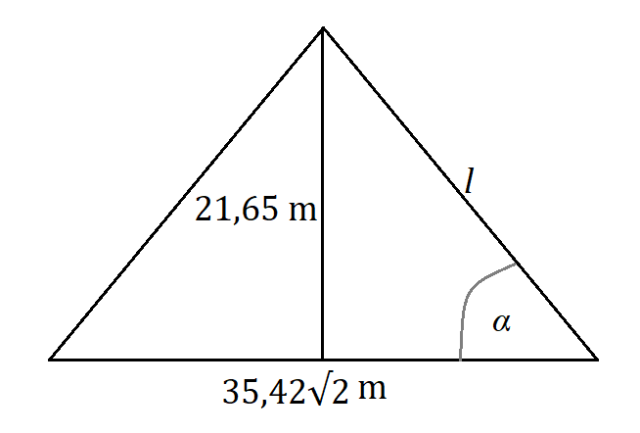
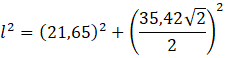
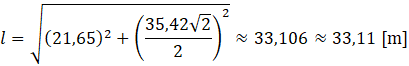

Liczba tafli w tym zadaniu jest nieistotna. Ważne są wymiary ostrosłupa. Narysuj sobie tę piramidę. Jej wysokość jest podana. Znasz również długość krawędzi podstawy. Aby wyznaczyć długość krawędzi bocznej, korzystasz z twierdzenia Pitagorasa. Przyprostokątne trójkąta prostokątnego to wysokość piramidy oraz połowa przekątnej podstawy, a przeciwprostokątna to szukana długość.

Zadanie 1.8.
16Zadanie 1.11.
17Zadanie 1.13.
17Zadanie Prosto do matury 5.
18Zadanie 2.1.
24Zadanie 2.5.
24Zadanie 2.8.
25Zadanie 2.9.
25Zadanie 2.11.
25Zadanie 2.12.
25Zadanie 2.13.
26Zadanie 2.14.
26Zadanie 2.15.
26Zadanie 3.1.
30Zadanie 3.2.
31Zadanie 3.3.
31Zadanie Prosto do matury 5.
33Zadanie 4.1.
42Zadanie 4.3.
42Zadanie 4.6.
42Zadanie 4.7.
42Zadanie 4.11.
42Zadanie 4.14.
43Zadanie 4.17.
43Zadanie 5.1.
56Zadanie 5.2.
56Zadanie 5.3.
56Zadanie 5.6.
56Zadanie 5.10.
57Zadanie 5.17.
57Zadanie 5.23.
58Zadanie 6.2.
69Zadanie 6.3.
69Zadanie 6.4.
69Zadanie 6.7.
69Zadanie 6.11.
69Zadanie 6.12.
69Zadanie 7.10.
82Zadanie 37.
90
