Masz wykazać, że trzy proste, które nie leżą w jednej płaszczyźnie, ale każda z dwóch się przecina, mają jeden wspólny punkt.
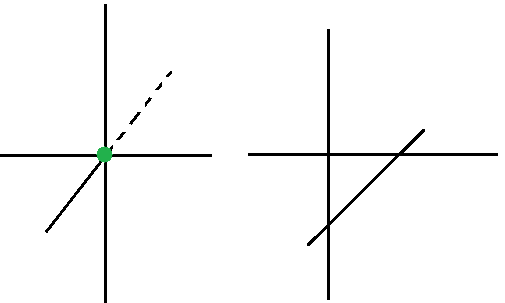
Jeśli każde dwie proste mają się przecinać, to znaczy, że wszystkie trzy przecinają się w jednym punkcie (rys. 1).

Zauważ (rys. 2), że gdyby trzecia prosta przecinała dwie pozostałe w dwóch punktach, to okazałoby się, że wszystkie trzy proste leżą w jednej płaszczyźnie, a z założenia tak nie jest.

Zadanie 1.8.
16Zadanie 1.11.
17Zadanie 1.13.
17Zadanie Prosto do matury 5.
18Zadanie 2.1.
24Zadanie 2.5.
24Zadanie 2.8.
25Zadanie 2.9.
25Zadanie 2.11.
25Zadanie 2.12.
25Zadanie 2.13.
26Zadanie 2.14.
26Zadanie 2.15.
26Zadanie 3.1.
30Zadanie 3.2.
31Zadanie 3.3.
31Zadanie Prosto do matury 5.
33Zadanie 4.1.
42Zadanie 4.3.
42Zadanie 4.6.
42Zadanie 4.7.
42Zadanie 4.11.
42Zadanie 4.14.
43Zadanie 4.17.
43Zadanie 5.1.
56Zadanie 5.2.
56Zadanie 5.3.
56Zadanie 5.6.
56Zadanie 5.10.
57Zadanie 5.17.
57Zadanie 5.23.
58Zadanie 6.2.
69Zadanie 6.3.
69Zadanie 6.4.
69Zadanie 6.7.
69Zadanie 6.11.
69Zadanie 6.12.
69Zadanie 7.10.
82Zadanie 37.
90
