Korzystając z danych, należy obliczyć względną niepewność pomiarową każdej wartości przyspieszenia ziemskiego oraz na ich podstawie stwierdzić, jakiego wahadła należy użyć, aby wynik był jak najdokładniejszy.
Dane:
![]()
![]()
Rozwiązanie:
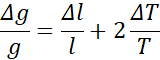
| Nr wahadła | 1 | 2 | 3 | 4 | 5 | 6 |
| Długość wahadła l [m] | 0,18 | 0,26 | 0,37 | 0,49 | 0,61 | 0,9 |
| Okres drgań T [s] | 0,87 | 1,03 | 1,24 | 1,42 | 1,57 | 1,8 |
| g [m/s^2] | 9,39 | 9,68 | 9,5 | 9,59 | 9,77 | 10,97 |
| niepewność | 0,057 | 0,046 | 0,037 | 0,032 | 0,029 | 0,024 |

Korzystając ze wzoru na niepewność względną pomiaru, obliczamy kolejne niepewności, widzimy, że im dłuższe wahadło tym niepewność jest mniejsza, a zatem dokładniejszy wynik otrzymamy, wtedy kiedy użyjemy dłuższego wahadła.

Zadanie 9.1.5.
135Zadanie 9.1.7.
136Zadanie 9.1.8.
136Zadanie 9.1.10.
136Zadanie 9.1.11.
137Zadanie 9.1.12.
137Zadanie 9.1.13.
137Zadanie 9.1.14.
137Zadanie 9.2.7.
144Zadanie 9.2.8.
144Zadanie 9.2.11.
145Zadanie 9.2.12.
145Zadanie 9.1.14.
145Zadanie 9.3.1
149Zadanie 9.3.7.
150Zadanie 9.3.8.
150Zadanie 9.3.10.
150Zadanie 9.3.11.
150Zadanie 9.3.12.
151Zadanie 9.3.14.
151Zadanie 9.4.2.
159Zadanie 9.4.10.
161Zadanie 9.4.17.
162Zadanie 1. Ruch drgający
174Zadanie 2. Suwnica bramowa
174Zadanie 3. Dwie sprężyny
175Zadanie 4. Winda towarowa
175Zadanie 5. Wahadło fizyczne
176
