Zadanie
Należy obliczyć czas, po którym energia kinetyczna i potencjalna będą sobie równe.
Rozwiązanie
Dane:
Szukane:
Rozwiązanie:
Wyjaśnienie
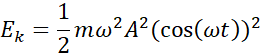
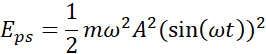
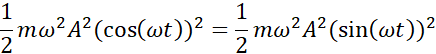
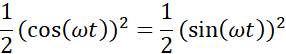
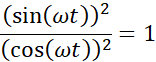
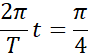
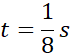
Korzystając z równania wychylenia podanego w treści, odczytujemy dane takie jak amplituda oraz okres, następnie korzystając ze wzorów na energię kinetyczną i potencjalna sprężystości zależnych od czasu obliczamy najkrótszy czas, po jakim energię będą sobie równe.
Fizyka - wybrane pytania
REKLAMA
Zadania z tego działu
9. Ruch drgający
135
9.1. Badanie ruchu drgającego. Drgania harmoniczne
135
Zadanie 9.1.5.
135Zadanie 9.1.7.
136Zadanie 9.1.8.
136Zadanie 9.1.10.
136Zadanie 9.1.11.
137Zadanie 9.1.12.
137Zadanie 9.1.13.
137Zadanie 9.1.14.
137
9.2. Drgania sprężyn
143
Zadanie 9.2.7.
144Zadanie 9.2.8.
144Zadanie 9.2.11.
145Zadanie 9.2.12.
145Zadanie 9.1.14.
145
9.3. Wahadło matematyczne
149
Zadanie 9.3.1
149Zadanie 9.3.7.
150Zadanie 9.3.8.
150Zadanie 9.3.10.
150Zadanie 9.3.11.
150Zadanie 9.3.12.
151Zadanie 9.3.14.
151
9.4. Energia w ruchu harmonicznym
159
Zadanie 9.4.2.
159Zadanie 9.4.10.
161Zadanie 9.4.17.
162
9.5. Drgania tłumione i wymuszone. Rezonans
166
Klasyka fizyki
170
Zadania maturalne
174
Zadanie 1. Ruch drgający
174Zadanie 2. Suwnica bramowa
174Zadanie 3. Dwie sprężyny
175Zadanie 4. Winda towarowa
175Zadanie 5. Wahadło fizyczne
176