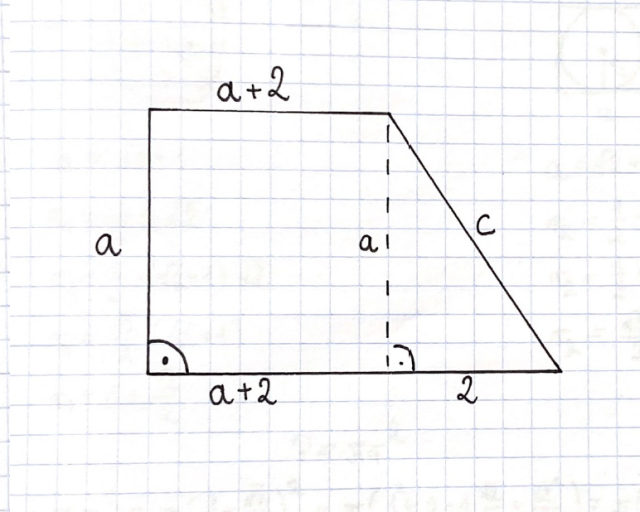
W tym zadaniu należy obliczyć obwód trapezu, którego pole jest równe 40 cm2 oraz który posiada bok prostopadły do obu podstaw krótszy od jednej z nich o 2 cm, a od drugiej o 4 cm.
Zrób rysunek pomocniczy:
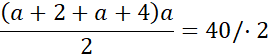
(2a + 6)a = 80 / - 80
2a2 + 6a – 80 = 0 / : 2
a2 + 3a – 40 = 0
a2 + 3a – 40 = a2 + 8a – 5a – 40 = a(a + 8) – 5(a + 8) = (a - 5)(a + 8)
(a - 5)(a + 8) = 0
a = 5 lub a = -8 → długość nie może być ujemna
52 + 22 = c2
c2 = 25 + 4 = 13
![]()
![]()

Wzór na pole trapezu to ![]()
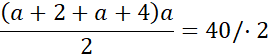
(2a + 6)a = 80 / - 80
2a2 + 6a – 80 = 0 / : 2
a2 + 3a – 40 = 0
Rozłóż wyrażenie na czynniki i wyciągnij wspólny przed nawias:
a2 + 3a – 40 = a2 + 8a – 5a – 40 = a(a + 8) – 5(a + 8) = (a - 5)(a + 8)
(a - 5)(a + 8) = 0
a = 5 lub a = -8 → długość nie może być ujemna
Oblicz długość ramienia trapezu. Skorzystaj z twierdzenia Pitagorasa a2 + b2 = c2, gdzie a i b to przyprostokątne, natomiast c to przeciwprostokątna trójkąta prostokątnego.
52 + 22 = c2
c2 = 25 + 4 = 13
![]()
Zapisz obwód:
![]()

Zadanie 1
14Zadanie 4
49Zadanie 6
49Zadanie 8
50Zadanie 9
50Zadanie 10
50Zadanie 13
50Zadanie 16
51Zadanie 18
51Zadanie 19
51Zadanie 20
52Zadanie 21
52Ćwiczenie A
53Zadanie 1
54Zadanie 2
54Zadanie 3
54Zadanie 4
54Zadanie 6
54Zadanie 10
55Ćwiczenie A
58Ćwiczenie D
58Zadanie 1
60Zadanie 2
60Zadanie 5
60Zadanie 9
60Zadanie 10
61Zadanie 12
61Zadanie 15
62Zadanie 19
62Zadanie 20
62Zadanie 22
63Ćwiczenie A
64Ćwiczenie C
67Zadanie 1
69Zadanie 8
70Zadanie 18
71Zadanie 20
71Zadanie 21
71Zadanie 26
72Zadanie D
76Zadanie 1
76Zadanie 3
77Zadanie 11
77Zadanie 14
78Zadanie 17
79Zadanie 19
79
