W tym zadaniu udowodnij twierdzenie napisane powyżej wzorując się na dowodzie twierdzenia o punkcie przecięcia symetralnych boków trójkąta.
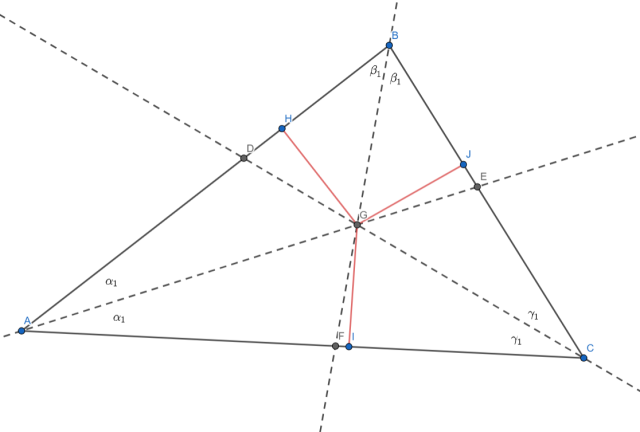
|IG| = |GJ|, |GJ| = |GH| oraz |GH| = |GI|, zatem dwusieczne kąta dowolnego trójkąta zawsze przecinają się w jednym punkcie.

Twierdzenie do udowodnienia: w każdym trójkącie dwusieczne kątów przecinają się w jednym punkcie.
Dowód:
Dwusieczna kąta to półprosta, która dzieli ten kąt na dwa kąty o równych miarach. Narysuj dowolny trójkąt i jego dwusieczne.
Czerwone odcinki to odległości punktu przecięcia dwusiecznych od ramion trójkąta. Dwusieczna to inaczej zbiór punktów należących do kąta i równo odległych od jego ramion. Wynika z tego, że |IG| = |GJ|, |GJ| = |GH| oraz |GH| = |GI|, zatem dwusieczne kąta dowolnego trójkąta zawsze przecinają się w jednym punkcie.

Zadanie 1
14Zadanie 4
49Zadanie 6
49Zadanie 8
50Zadanie 9
50Zadanie 10
50Zadanie 13
50Zadanie 16
51Zadanie 18
51Zadanie 19
51Zadanie 20
52Zadanie 21
52Ćwiczenie A
53Zadanie 1
54Zadanie 2
54Zadanie 3
54Zadanie 4
54Zadanie 6
54Zadanie 10
55Ćwiczenie A
58Ćwiczenie D
58Zadanie 1
60Zadanie 2
60Zadanie 5
60Zadanie 9
60Zadanie 10
61Zadanie 12
61Zadanie 15
62Zadanie 19
62Zadanie 20
62Zadanie 22
63Ćwiczenie A
64Ćwiczenie C
67Zadanie 1
69Zadanie 8
70Zadanie 18
71Zadanie 20
71Zadanie 21
71Zadanie 26
72Zadanie D
76Zadanie 1
76Zadanie 3
77Zadanie 11
77Zadanie 14
78Zadanie 17
79Zadanie 19
79
