W tym zadaniu oblicz jakie są odległości punktu d od poszczególnych boków trójkąta wiedząc, że boki trójkąta ostrokątnego mają długości a, b i c, a symetralne boków przecinają się w punkcie, którego odległość od wierzchołków trójkąta jest równa d.
Zrób rysunek pomocniczy:
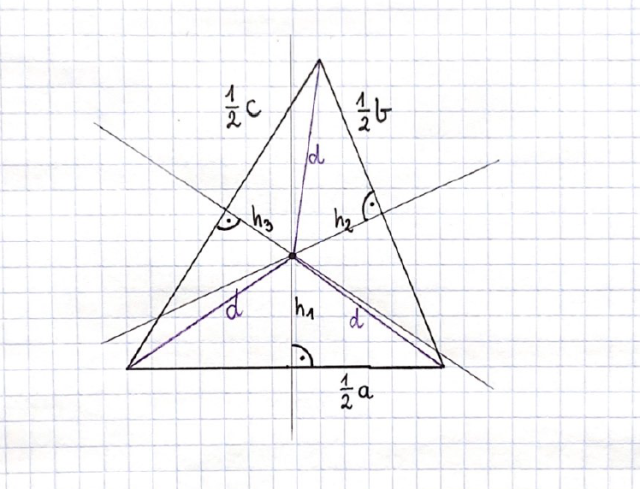
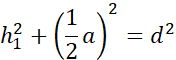
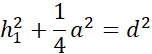
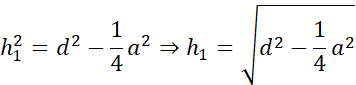
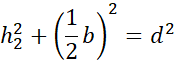
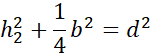
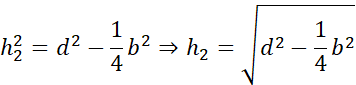
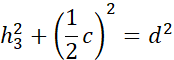
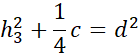
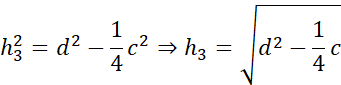

Symetralna dzieli odcinek na pół i pada na niego pod kątem prostym. Zauważ, że po narysowaniu symetralnych i odcinków łączących wierzchołki trójkąta z punktem przecięcia symetralnych powstały trójkąty prostokątne. Wyznacz h1, h2 i h3 korzystając z twierdzenia Pitagorasa: a2 + b2 = c2, gdzie a i b to przyprostokątne, natomiast c to przeciwprostokątna trójkąta prostokątnego.
Działania dla pierwszego trójkąta:
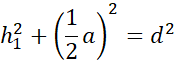
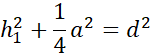
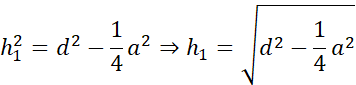
Działania dla drugiego trójkąta:
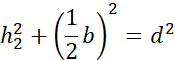
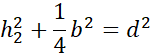
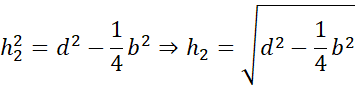
Działania dla trzeciego trójkąta:
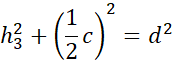
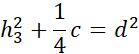
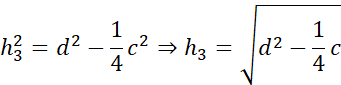

Zadanie 1
14Zadanie 4
49Zadanie 6
49Zadanie 8
50Zadanie 9
50Zadanie 10
50Zadanie 13
50Zadanie 16
51Zadanie 18
51Zadanie 19
51Zadanie 20
52Zadanie 21
52Ćwiczenie A
53Zadanie 1
54Zadanie 2
54Zadanie 3
54Zadanie 4
54Zadanie 6
54Zadanie 10
55Ćwiczenie A
58Ćwiczenie D
58Zadanie 1
60Zadanie 2
60Zadanie 5
60Zadanie 9
60Zadanie 10
61Zadanie 12
61Zadanie 15
62Zadanie 19
62Zadanie 20
62Zadanie 22
63Ćwiczenie A
64Ćwiczenie C
67Zadanie 1
69Zadanie 8
70Zadanie 18
71Zadanie 20
71Zadanie 21
71Zadanie 26
72Zadanie D
76Zadanie 1
76Zadanie 3
77Zadanie 11
77Zadanie 14
78Zadanie 17
79Zadanie 19
79
