W tym zadaniu oblicz na jaką wysokość nad powierzchnię wody można by unieść środek liny na 25-metrowym basenie pływackim, gdyby jej długość zwiększono o 1m.
12,52 + x2 = 132
156,25 + x2 = 169 /-156,25
x2 = 12,75
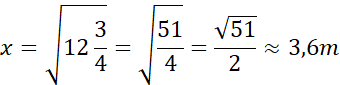

Zauważ, że po podniesieniu liny do góry powstaną dwa trójkąty prostokątne: każdy o wysokości x, przeciwprostokątnej 13 (ponieważ długość liny wynosi 26m i musisz ją podzielić na 2 części) oraz podstawie o długości 25m : 2 = 12,5m. Zapisz dla tego trójkąta twierdzenie Pitagorasa:
12,52 + x2 = 132
156,25 + x2 = 169 /-156,25
x2 = 12,75
Spierwiastkuj obie strony i zaokrąglij wynik.
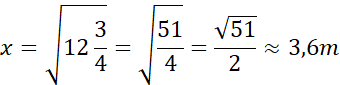

Zadanie 1
14Zadanie 4
49Zadanie 6
49Zadanie 8
50Zadanie 9
50Zadanie 10
50Zadanie 13
50Zadanie 16
51Zadanie 18
51Zadanie 19
51Zadanie 20
52Zadanie 21
52Ćwiczenie A
53Zadanie 1
54Zadanie 2
54Zadanie 3
54Zadanie 4
54Zadanie 6
54Zadanie 10
55Ćwiczenie A
58Ćwiczenie D
58Zadanie 1
60Zadanie 2
60Zadanie 5
60Zadanie 9
60Zadanie 10
61Zadanie 12
61Zadanie 15
62Zadanie 19
62Zadanie 20
62Zadanie 22
63Ćwiczenie A
64Ćwiczenie C
67Zadanie 1
69Zadanie 8
70Zadanie 18
71Zadanie 20
71Zadanie 21
71Zadanie 26
72Zadanie D
76Zadanie 1
76Zadanie 3
77Zadanie 11
77Zadanie 14
78Zadanie 17
79Zadanie 19
79
