W tym zadaniu trzeba obliczyć obwód trapezu prostokątnego o polu 12, którego krótsza podstawa i wysokość mają równe długości, a różnica długości podstaw wynosi 2.
Krótsza podstawa: a
Wysokość: h = a
Dłuższa podstawa: b = a + 2
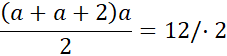
(2a + 2)a = 24 / - 24
2a2 + 2a – 24 = 0 / : 2
a2 + a – 12 = 0
![]()
![]()
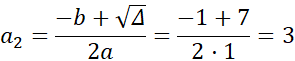
33 + 22 = c2
c2 = 9 + 4 = 13
![]()
![]()

Krótsza podstawa: a
Wysokość: h = a
Dłuższa podstawa: b = a + 2
Wzór na pole trapezu to ![]()
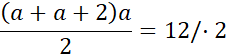
(2a + 2)a = 24 / - 24
2a2 + 2a – 24 = 0 / : 2
a2 + a – 12 = 0
Wyznacz a ze wzoru na deltę:
![]()
![]()
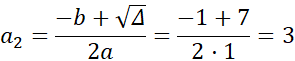
Oblicz długość ramienia trapezu korzystając z trójkąta prostokątnego o boku h = 3, b = 2 oraz przeciwprostokątnej c. Skorzystaj z twierdzenia Pitagorasa a2 + b2 = c2, gdzie a i b to przyprostokątne, natomiast c to przeciwprostokątna trójkąta prostokątnego.
33 + 22 = c2
c2 = 9 + 4 = 13
![]()
Zapisz obwód trapezu:
![]()

Zadanie 1
14Zadanie 4
49Zadanie 6
49Zadanie 8
50Zadanie 9
50Zadanie 10
50Zadanie 13
50Zadanie 16
51Zadanie 18
51Zadanie 19
51Zadanie 20
52Zadanie 21
52Ćwiczenie A
53Zadanie 1
54Zadanie 2
54Zadanie 3
54Zadanie 4
54Zadanie 6
54Zadanie 10
55Ćwiczenie A
58Ćwiczenie D
58Zadanie 1
60Zadanie 2
60Zadanie 5
60Zadanie 9
60Zadanie 10
61Zadanie 12
61Zadanie 15
62Zadanie 19
62Zadanie 20
62Zadanie 22
63Ćwiczenie A
64Ćwiczenie C
67Zadanie 1
69Zadanie 8
70Zadanie 18
71Zadanie 20
71Zadanie 21
71Zadanie 26
72Zadanie D
76Zadanie 1
76Zadanie 3
77Zadanie 11
77Zadanie 14
78Zadanie 17
79Zadanie 19
79
