W tym zadaniu oblicz wysokość trójkąta równoramiennego ABC opuszczoną na podstawę wiedząc, że w tym trójkącie środkowe AM i BN poprowadzone do ramion przecinają się w punkcie P, obwód czworokąta MCNP jest równy 10, a obwód trójkąta BCP jest równy 13.
Zrób rysunek pomocniczy:
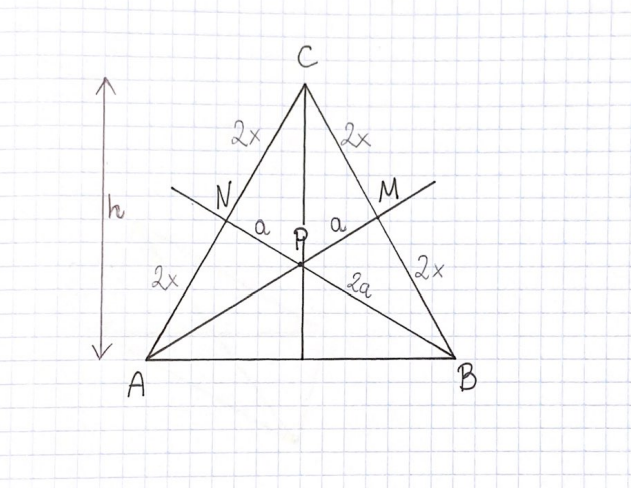
|PN| = |PM| = a
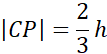
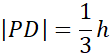
Obwód MCNP:
2x + 2x + 2a = 10
4x + 2a = 10
Obwód BCP:
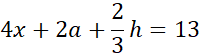
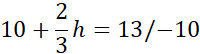
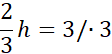
2h = 9 / : 2
h = 4,5

Środkowa trójkąta to odcinek łączący wierzchołek trójkąta ze środkiem przeciwległego boku. Zauważ, że wysokość trójkąta równoramiennego padająca na podstawę AB również jest środkową. W każdym trójkącie środkowe przecinają się jednym punkcie zwanym środkiem ciężkości i dzielą się na odcinki w stosunku 1 : 2. Jest to trójkąt równoramienny, więc
|PN| = |PM| = a
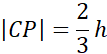
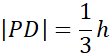
Obwód MCNP:
2x + 2x + 2a = 10
4x + 2a = 10
Obwód BCP:
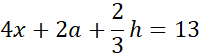
Podstaw wartość 10 za wyrażenie 4x + 2a
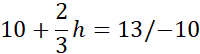
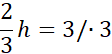
2h = 9 / : 2
h = 4,5

Zadanie 1
14Zadanie 4
49Zadanie 6
49Zadanie 8
50Zadanie 9
50Zadanie 10
50Zadanie 13
50Zadanie 16
51Zadanie 18
51Zadanie 19
51Zadanie 20
52Zadanie 21
52Ćwiczenie A
53Zadanie 1
54Zadanie 2
54Zadanie 3
54Zadanie 4
54Zadanie 6
54Zadanie 10
55Ćwiczenie A
58Ćwiczenie D
58Zadanie 1
60Zadanie 2
60Zadanie 5
60Zadanie 9
60Zadanie 10
61Zadanie 12
61Zadanie 15
62Zadanie 19
62Zadanie 20
62Zadanie 22
63Ćwiczenie A
64Ćwiczenie C
67Zadanie 1
69Zadanie 8
70Zadanie 18
71Zadanie 20
71Zadanie 21
71Zadanie 26
72Zadanie D
76Zadanie 1
76Zadanie 3
77Zadanie 11
77Zadanie 14
78Zadanie 17
79Zadanie 19
79
