W tym zadaniu oblicz długości zaznaczonych łamanych, korzystając z informacji podanych pod rysunkami, na których przedstawiono prostokąt, równoległobok i figurę złożoną z dwóch jednakowych trapezów równoramiennych.
Prostokąt:
72 + 42 = c2
c2 = 49 + 16 = 65 ⇒![]()
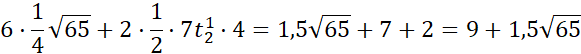
Równoległobok:
3 ∙ 0,25 ∙ 9 + 4 ∙ 0,25 ∙ 7 = 6,75 + 7 = 13,75
Figura trzecia:
2 ∙ 7 = 14

Prostokąt:
Oblicz długość przekątnej prostokąta korzystając z twierdzenia Pitagorasa a2 + b2 = c2, gdzie a i b to przyprostokątne, natomiast c to przeciwprostokątna trójkąta prostokątnego.
72 + 42 = c2
c2 = 49 + 16 = 65 ⇒![]()
Na łamaną składa się 6 odcinków o długości 0,25c 2 odcinków o długości 0,5|AB| i jednego o długości 0,5|BC|. Zapisz działanie:
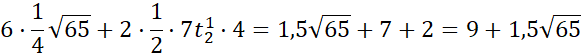
Równoległobok:
Na łamaną składają się 3 odcinki o długości 0,25|EG| i 4 odcinki o długość 0,25|FH|. Zapisz działanie:
3 ∙ 0,25 ∙ 9 + 4 ∙ 0,25 ∙ 7 = 6,75 + 7 = 13,75
Figura trzecia:
Zauważ, że łamana składa się z dwóch odcinków |KO|. 2 ∙ 7 = 14

Zadanie 1
14Zadanie 4
49Zadanie 6
49Zadanie 8
50Zadanie 9
50Zadanie 10
50Zadanie 13
50Zadanie 16
51Zadanie 18
51Zadanie 19
51Zadanie 20
52Zadanie 21
52Ćwiczenie A
53Zadanie 1
54Zadanie 2
54Zadanie 3
54Zadanie 4
54Zadanie 6
54Zadanie 10
55Ćwiczenie A
58Ćwiczenie D
58Zadanie 1
60Zadanie 2
60Zadanie 5
60Zadanie 9
60Zadanie 10
61Zadanie 12
61Zadanie 15
62Zadanie 19
62Zadanie 20
62Zadanie 22
63Ćwiczenie A
64Ćwiczenie C
67Zadanie 1
69Zadanie 8
70Zadanie 18
71Zadanie 20
71Zadanie 21
71Zadanie 26
72Zadanie D
76Zadanie 1
76Zadanie 3
77Zadanie 11
77Zadanie 14
78Zadanie 17
79Zadanie 19
79
