W tym zadaniu uzasadnij, że największy kąt czworokąta CNPM ma miarę 135° wiedząc, że dwusieczne AM i BM kątów ostrych trójkąta prostokątnego ABC przecinają się w punkcie P, a punkty M i N leżą na bokach trójkąta.
Zrób rysunek pomocniczy:
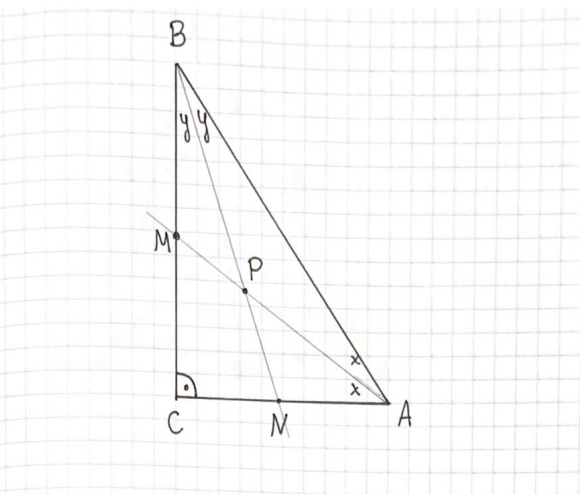
2x + 2y + 90 = 180 / - 90
2x + 2y = 90 / : 2
x + y = 45
x + y + APB = 180
45 + APB = 180 / - 45
APB = 135 = kąt MNP

Dwusieczna to odcinek dzielący kąt na pół. Zatem zauważ, że w trójkącie ABC przy wierzchołku A kąt ma miarę 2x, a przy wierzchołku B kąt ma miarę 2y.
Kąty APB oraz MNP są wierzchołkowe, zatem są sobie równe.
Suma miar kątów w trójkącie wynosi 180 stopni, dlatego zapisz dla trójkąta ABC:
2x + 2y + 90 = 180 / - 90
2x + 2y = 90 / : 2
x + y = 45
Zapisz równanie dla trójkąta APB:
x + y + APB = 180
45 + APB = 180 / - 45
APB = 135 = kąt MNP

Zadanie 1
14Zadanie 4
49Zadanie 6
49Zadanie 8
50Zadanie 9
50Zadanie 10
50Zadanie 13
50Zadanie 16
51Zadanie 18
51Zadanie 19
51Zadanie 20
52Zadanie 21
52Ćwiczenie A
53Zadanie 1
54Zadanie 2
54Zadanie 3
54Zadanie 4
54Zadanie 6
54Zadanie 10
55Ćwiczenie A
58Ćwiczenie D
58Zadanie 1
60Zadanie 2
60Zadanie 5
60Zadanie 9
60Zadanie 10
61Zadanie 12
61Zadanie 15
62Zadanie 19
62Zadanie 20
62Zadanie 22
63Ćwiczenie A
64Ćwiczenie C
67Zadanie 1
69Zadanie 8
70Zadanie 18
71Zadanie 20
71Zadanie 21
71Zadanie 26
72Zadanie D
76Zadanie 1
76Zadanie 3
77Zadanie 11
77Zadanie 14
78Zadanie 17
79Zadanie 19
79
