Prosto do matury 3. Zakres podstawowy. Podręcznik - rozwiązania i odpowiedzi

Podręcznik, Wydawnictwo: Nowa Era

Zadanie 4. - strona 35

Ustal prawdziwość podanych zdań w trójkącie prostokątnym jedna z przyprostokątnych jest dwa razy krótsza od przeciwprostokątnej.
A.Jeden z kątów ostrych tego trójkąta jest dwa razy mniejszy od drugiego kąta ostrego.
B.Dwusieczna kąta prostego dzieli przeciwprostokątną na dwa odcinki, z których jeden jest dwa razy krótszy od drugiego.
C.Stosunek promienia okręgu opisanego na tym trójkącie do promienia okręgu wpisanego w ten trójkąt wynosi $1 + \sqrt{3}$ ..

$\frac{a \sqrt{3}}{a} = \frac{| AD |}{| CD |}$ $\frac{| AD |}{| C D |} = \sqrt{3}$ $P = \frac{1}{2} a \cdot a \sqrt{3} = \frac{a^{2} \sqrt{3}}{2}$ $\frac{a + a \sqrt{3} + 2 a}{2} \cdot r = \frac{a^{2} \sqrt{3}}{2}$ $r (3 a + \sqrt{3} a) = a^{2} \sqrt{3}$ $r = \frac{\sqrt{3} a}{3 + \sqrt{3}}$ $\frac{a \cdot a \sqrt{3} \cdot 2 a}{4 R} = \frac{a^{2} \sqrt{3}}{2}$ $R = \frac{a \sqrt{3}}{\sqrt{3}} = a$ $\frac{R}{r} = \frac{a}{\frac{\sqrt{3} a}{3 + \sqrt{3}}} = \frac{3 + \sqrt{3}}{\sqrt{3}} = \frac{3 \sqrt{3} + 3}{3} = \sqrt{3} + 1$

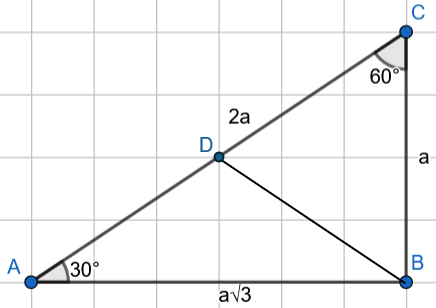
Odp. P,F,P

Zauważ, że trójkąt prostokątny o podanych kątach jest szczególny – długość boku naprzeciwko największego kąta jest dwa razy większa od długości boku naprzeciwko najmniejszego kąta, a długość boku leżącego naprzeciwko środowego kąta jest $\sqrt{3}$ razy dłuższa od długości najkrótszego boku. Następnie skorzystaj z twierdzenia o dwusiecznej: $\frac{x}{y} = \frac{a}{b}$ , gdzie $x, y$ to odcinki na jakie dwusieczna dzieli bok trójkąta, a $a, b$ to jego pozostałe boki.Na koniec skorzystaj ze wzoru Herona na pole trójkąta: $P = \sqrt{p (p - a) (p - b) (p - c)}$ , gdzie $p$ to połowa obwodu, a $a, b, c$ to boki trójkąta, na pole trójkąta z promieniami opisanym: $P = \frac{abc}{4 R}$ oraz wpisanym: $P = pr$ w trójkąt i na tej podstawie wyznacz długości promieni i ich stosunek.

Zadanie 4, strona 51, MATeMAtyka 1. Karty pracy ucznia. Zakres podstawowy

Zadanie 9., strona 70, Matematyka. Klasa 7. Zbiór zadań – rozwiązania i odpowiedzi

Zadanie 3, strona 266, Matematyka wokół nas. Klasa 6. Podręcznik – rozwiązania i odpowiedzi

Zadanie Prosto do matury 3, strona 142, Matematyka. Prosto do matury. Klasa 1. Zakres podstawowy i rozszerzony. Podręcznik - rozwiązania i odpowiedzi

Ćwiczenie 3, strona 152, Matematyka wokół nas. Klasa 4. Podręcznik - rozwiązania i odpowiedzi

Zadanie 12, strona 86, Matematyka z plusem. Klasa 8. Podręcznik – rozwiązania i odpowiedzi

Zadanie 10.9., strona 273, Matematyka. Prosto do matury. Klasa 1. Zakres podstawowy i rozszerzony. Podręcznik - rozwiązania i odpowiedzi

Ćwiczenie 2, strona 150, Matematyka z kluczem. Klasa 5. Podręcznik. Część 1 - rozwiązania i odpowiedzi

Zadanie 2., strona 180, Prosto do matury. Klasa 3. Zakres podstawowy. Podręcznik - rozwiązania i odpowiedzi

Zadanie 10., strona 24, Matematyka. Klasa 4. Podręcznik. Zakres rozszerzony – rozwiązania i odpowiedzi

Zadanie 1.1.

10

10

10

10

10

Zadanie 1.2.

10

10

10

10

10

Zadanie 1.3.

10

10

10

10

10

10

11

Zadanie 1.8.

11

11

11

11

11

Zadanie 1.9.

11

11

11

11

11

11

11

Zadanie 1.10.

11

11

11

11

Zadanie 1.12.

11

11

11

11

11

Zadanie 1.13.

11

11

11

11

11

11

11

11

18

Zadanie 2.2.

18

18

18

18

18

18

Zadanie 2.4.

18

18

18

18

18

18

18

18

Zadanie 2.9.

19

19

19

19

19

19

19

19

19

19

19

19

Zadanie 2.19.

19

19

19

19

20

20

20

20

20

20

20

20

Zadanie 3.1.

24

24

24

24

24

24

24

24

Zadanie 3.5.

24

24

24

24

24

Zadanie 3.6.

24

24

24

24

24

24

25

25

25

Zadanie 3.11.

25

25

25

25

25

25

25

25

25

25

25

25

25

26

26

26

26

26

26

26

26

26

26

32

32

33

33

33

Zadanie 4.6.

33

33

33

33

33

33

33

33

33

33

33

33

33

34

34

34

Zadanie 4.18.

34

34

34

Zadanie 4.19.

34

34

34

34

34

34

34

34

34

35

35

35

35

35

35

35

35

36

36

36

36

36

36

36

36

36

37

37

37

37

37

37

37

37

37

38

38

38

Zadanie 22.

38

38

38

38

38

38

38

Zadanie 27.

38

38

38

38

38

38

Pełny spis treści