Podana jest funkcja
![]() . Wyznacz jej przedziały monotoniczności.
. Wyznacz jej przedziały monotoniczności.
Wierzchołek paraboli:
![]()
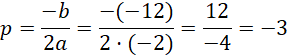
Zatem:
![]()
Skoro
![]() , to parabola ma ramiona skierowane w dół.
, to parabola ma ramiona skierowane w dół.
Zatem:
Funkcja
![]() jest rosnąca dla
jest rosnąca dla
![]()
Funkcja
![]() jest malejąca dla
jest malejąca dla
![]()

Najpierw wyznacz pierwszą współrzędną wierzchołka paraboli. Skorzystaj z zależności, że dla funkcji kwadratowej w postaci ogólnej
![]() parabola ma wierzchołek w punkcie
parabola ma wierzchołek w punkcie
![]() . Współrzędną p możemy wyznaczyć ze wzoru:
. Współrzędną p możemy wyznaczyć ze wzoru:
![]() . Następnie zauważ, że współczynnik a jest mniejszy od zera, zatem parabola będzie skierowana ramionami do dołu. Oznacza to, że w przedziale
. Następnie zauważ, że współczynnik a jest mniejszy od zera, zatem parabola będzie skierowana ramionami do dołu. Oznacza to, że w przedziale
![]() funkcja będzie rosnąca, a w przedziale
funkcja będzie rosnąca, a w przedziale
![]() będzie malejąca.
będzie malejąca.

Zadanie 1.4
407Zadanie 1.5
407Zadanie 1.6
407Zadanie 1.7
407Zadanie 1.8
408Zadanie 1.10
408Zadanie 1.11
408Zadanie 1.16
409Zadanie 2.4
414Zadanie 2.5
414Zadanie 2.6
414Zadanie 2.7
415Zadanie 2.8
415Zadanie 2.9
415Zadanie 2.10
415Zadanie 2.11
415Zadanie 2.12
415Zadanie 2.13
415Zadanie 2.14
416Zadanie 2.18
416Zadanie 2.19
416Zadanie 2.20
416Zadanie 2.21
416Zadanie 2.22
417Zadanie 2.23
417Zadanie 3.8
423Zadanie 3.9
423Zadanie 3.10
423Zadanie 3.11
423Zadanie 3.12
423Zadanie 3.13
424Zadanie 3.14
424Zadanie 3.15
424Zadanie 3.16
424Zadanie 3.20
424Zadanie 3.23
425Zadanie 3.24
425Zadanie 4.22
430Zadanie 4.23
430Zadanie 4.24
430Zadanie 4.27
431Zadanie 4.30
431Zadanie 4.32
431Zadanie 4.35
431Zadanie 4.41
432Zadanie 4.42
432
