Wybierz spośród podanych funkcję, której wykres ma identyczną oś symetrii do osi symetrii wykresu funkcji zadanej wzorem
![]() .
.
A.
![]()
B.
![]()
C.
![]()
D.
![]()
Oś symetrii podanej funkcji:
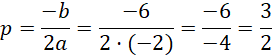
Zatem:
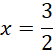
Osie symetrii funkcji w odpowiedziach:
A:

Zatem:
![]()
B:
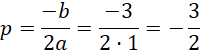
Zatem:
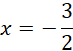
C:
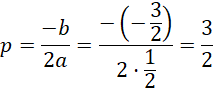
Zatem:
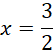
D:

Zatem:
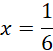
Odp.: C.
![]()

Skorzystaj z zależności, że dla funkcji kwadratowej w postaci ogólnej
![]() parabola ma wierzchołek w punkcie
parabola ma wierzchołek w punkcie
![]() . Współrzędną p możemy wyznaczyć ze wzoru:
. Współrzędną p możemy wyznaczyć ze wzoru:
![]() . Zwróć uwagę, że oś symetrii przechodzi przez wierzchołek paraboli i ma równanie
. Zwróć uwagę, że oś symetrii przechodzi przez wierzchołek paraboli i ma równanie
![]() , gdzie p to pierwsza współrzędna wierzchołka paraboli. Wyznacz pierwszą współrzędną wierzchołków parabol podanej funkcji kwadratowej oraz podanych w odpowiedziach funkcjach. Znajdź taką funkcję, której pierwsza współrzędna wierzchołka paraboli jest identyczna do pierwszej współrzędnej paraboli
, gdzie p to pierwsza współrzędna wierzchołka paraboli. Wyznacz pierwszą współrzędną wierzchołków parabol podanej funkcji kwadratowej oraz podanych w odpowiedziach funkcjach. Znajdź taką funkcję, której pierwsza współrzędna wierzchołka paraboli jest identyczna do pierwszej współrzędnej paraboli
![]() .
.

Zadanie 1.4
407Zadanie 1.5
407Zadanie 1.6
407Zadanie 1.7
407Zadanie 1.8
408Zadanie 1.10
408Zadanie 1.11
408Zadanie 1.16
409Zadanie 2.4
414Zadanie 2.5
414Zadanie 2.6
414Zadanie 2.7
415Zadanie 2.8
415Zadanie 2.9
415Zadanie 2.10
415Zadanie 2.11
415Zadanie 2.12
415Zadanie 2.13
415Zadanie 2.14
416Zadanie 2.18
416Zadanie 2.19
416Zadanie 2.20
416Zadanie 2.21
416Zadanie 2.22
417Zadanie 2.23
417Zadanie 3.8
423Zadanie 3.9
423Zadanie 3.10
423Zadanie 3.11
423Zadanie 3.12
423Zadanie 3.13
424Zadanie 3.14
424Zadanie 3.15
424Zadanie 3.16
424Zadanie 3.20
424Zadanie 3.23
425Zadanie 3.24
425Zadanie 4.22
430Zadanie 4.23
430Zadanie 4.24
430Zadanie 4.27
431Zadanie 4.30
431Zadanie 4.32
431Zadanie 4.35
431Zadanie 4.41
432Zadanie 4.42
432
